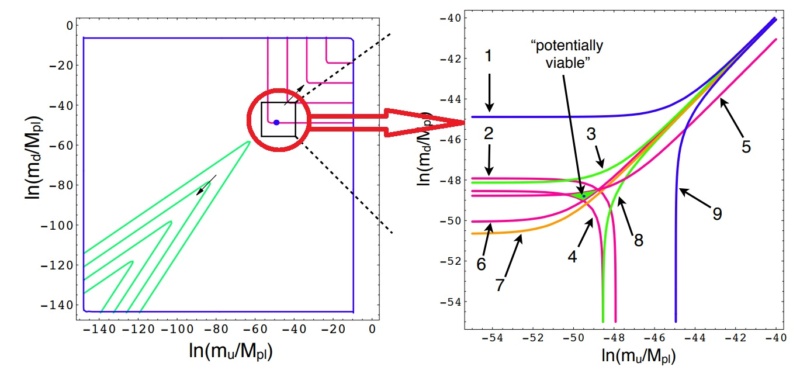
The Young Earth Creationist (YEC) model proposes a significantly shorter timescale for the formation and evolution of the universe compared to conventional cosmological models. Despite this difference, the fundamental laws of physics and the properties of matter and energy must still be finely tuned to allow for stable structures and life-supporting conditions. This precise tuning of cosmic parameters is essential, regardless of the specific cosmological model or proposed timescales. Even within a YEC framework, a balance of fundamental constants and parameters remains crucial. Parameters such as primordial fluctuations, matter-antimatter symmetry, the low-entropy state of the universe, dimensionality, curvature of the universe, neutrino background temperature, and the photon-to-baryon ratio could be relevant for understanding initial conditions and the formation of structures. Additionally, the fine-tuning of parameters related to the energy density and vacuum energy of the universe may be necessary in the YEC model. While the YEC model might not incorporate dark energy or vacuum energy as described in the standard cosmological model, it would still require a form of expansion or creation process. This process may necessitate the fine-tuning of parameters analogous to the energy scale, duration, potential energy density function, and the dynamics of expansion or creation. Fundamental constants like the speed of light and Planck's constant, which govern the behavior of electromagnetic radiation and quantum mechanics, are intrinsic to the universe's fabric. They are essential for the stability of atoms, subatomic particles, and celestial dynamics, even within the shorter timescales proposed by the YEC model. Regardless of the mechanisms or timescales proposed by the YEC cosmological model, the fundamental laws of physics and the properties of matter and energy must be precisely tuned to support stable structures and life. The list of parameters requiring fine-tuning remains largely the same, even if their relative significance may vary within the YEC framework. Further investigation and development of the YEC model would be needed to determine the applicability of fine-tuning parameters from the standard cosmological model.
References Chapter 4
1. Gribbin, J. (1991). Cosmic Coincidences: Dark Matter, Mankind and Anthropic Cosmology. Link. (This book explores the concept of cosmic coincidences and the anthropic principle, discussing the fine-tuning of the universe for life.)
2. Hawking, S. (1996). The Illustrated Brief History of Time, Updated and Expanded Edition. Link. (This classic book by Stephen Hawking provides an accessible introduction to cosmology and the nature of time, touching on topics related to the fine-tuning of the universe.)
3. Siegel, E. (2019). The Universe Really Is Fine-Tuned, And Our Existence Is The Proof. Link. (This article argues that the fine-tuning of the universe for life is a scientific fact, and our existence is evidence of this fine-tuning.)
4. Barnes, L.A. (2012). The Fine-Tuning of the Universe for Intelligent Life. Link. (This paper provides a comprehensive overview of the fine-tuning of the universe's laws, constants, and initial conditions necessary for the existence of intelligent life.)
5. Lemley, B. (2000). Why is There Life? Because, says Britain's Astronomer Royal, you happen to be in the right universe. Link. (This article discusses the fine-tuning of the universe for life, as explained by the Astronomer Royal of Britain.)
6. Rees, M. (1999). Just Six Numbers: The Deep Forces that Shape the Universe. Basic Books. Link. (In this seminal work, renowned cosmologist Martin Rees examines the six fundamental numbers that govern the universe's structures and properties, highlighting the extraordinary fine-tuning required for life to emerge.)
7. Vangioni, E. (2017). Cosmic origin of the chemical elements rarety in nuclear astrophysics. Link. (This paper discusses the cosmic origin of chemical elements and their rarity, which is related to the fine-tuning of nuclear physics.)
8. Penrose, R. (1994). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics (p. 179). Link. (This book by Roger Penrose explores the nature of consciousness, quantum mechanics, and the laws of physics, touching on topics related to the fine-tuning of the universe.)
9. Doko, E. (2019). Does Fine-Tuning Need an Explanation? Link. (This paper discusses whether the fine-tuning of the universe requires an explanation and examines various philosophical perspectives on the issue.)
10. Hughes, S. (2005). Fundamental forces. Link. (These lecture notes provide an introduction to the fundamental forces of nature, which are crucial in understanding the fine-tuning of the universe.)
11. BBC. (2024). The Dark Universe: Why we're about to solve the biggest mystery in science. Link. (This article discusses the ongoing efforts to understand the nature of dark matter and dark energy, which are related to the fine-tuning of the universe.)
12. Borde, A., Guth, A.H., & Vilenkin, A. (2003). Inflationary Spacetimes Are Incomplete in Past Directions. Link. (This paper presents a theorem that suggests that inflationary spacetimes must have a beginning, which has implications for the fine-tuning of the universe.)
13. Weinberg, S. (1993). The First Three Minutes. Link. (This classic book by Steven Weinberg provides an accessible account of the early universe, including discussions of nucleosynthesis and the fine-tuning of fundamental constants.)
14. Steigman, G. (2007). Neutrinos and BBN (and the CMB). Link. (This paper discusses the role of neutrinos in Big Bang nucleosynthesis and their impact on the cosmic microwave background, which is related to the fine-tuning of the universe.)
15. Linde, A. (2017). Particle Physics and Inflationary Cosmology (1st Edition). Link. (This book by Andrei Linde provides a comprehensive overview of inflationary cosmology and its connections to particle physics, including discussions of the fine-tuning of the universe.)
16. Lyth, D.H., & Riotto, A. (1999). Particle physics models of inflation and the cosmological density perturbation. Link. (This review paper discusses various particle physics models of inflation and their predictions for the cosmological density perturbation, which is related to the fine-tuning of the universe.)
17. Lyth, D.H. (1997). What would we learn by detecting a gravitational wave signal in the cosmic microwave background anisotropy? Link. (This paper explores the implications of detecting gravitational waves in the cosmic microwave background, which could provide insights into the inflationary epoch and the fine-tuning of the universe.)
18. Martin, J., Ringeval, C., Trotta, R., & Vennin, V. (2014). The Best Inflationary Models After Planck. Link. (This paper analyzes the constraints on inflationary models from the Planck satellite data, which has implications for the fine-tuning of the universe.)
19. Wands, D. (1994). Duality invariance of cosmological perturbation spectra. Link. (This paper discusses the duality invariance of cosmological perturbation spectra, which is relevant for understanding the fine-tuning of the universe.)
20. Liddle, A.R. (1999). An introduction to cosmological inflation. Link. (This review provides an introduction to the theory of cosmological inflation, which is crucial for understanding the fine-tuning of the universe's initial conditions.)
21. Planck Collaboration. (2018). Planck 2018 results. X. Constraints on inflation. Link. (This paper presents the constraints on inflationary models from the Planck 2018 data release, which has implications for the fine-tuning of the universe.)
23. Particle Data Group. (2023). Review on Inflation. Link. (This review by the Particle Data Group discusses the latest developments in inflationary theory, including the tensor-to-scalar ratio and its implications for single-field slow-roll models.)
24. Palma, G.A., & Sypsas, S. (2017). Determining the Scale of Inflation from Cosmic Vectors. Link. (This paper presents a novel approach to determining the scale of inflation, independent of the tensor-to-scalar ratio, offering insights into the inflationary scale from different perspectives.)
25. Weinberg, S. (1989). The cosmological constant problem. Reviews of Modern Physics, 61(1), 1-23. [url=https://isidore.co/misc/Physics papers and books/Recent Papers/Dark Energy Reviews/1. Weinberg (1989).pdf]Link[/url] (This seminal paper by Steven Weinberg discusses the cosmological constant problem, which is a significant fine-tuning issue in cosmology.)
26. Peebles, P.J.E., & Ratra, B. (2003). The cosmological constant and dark energy. Reviews of Modern Physics, 75(2), 559-606. (This review paper provides a comprehensive discussion of the cosmological constant and dark energy, which are related to the fine-tuning of the universe.)
27. Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., Scolnic, D. (2019). Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. The Astrophysical Journal, 876(1), 85. Link
28. Zwart, S. (2012). Personal Observations on Allan Sandage's Spiritual Journey. Reasons to Believe. Link (This blog post provides personal insights into the spiritual journey of the renowned astronomer Allan Sandage, including his views on the relationship between science and faith.)
29. Soter, S. (2010). Allan R. Sandage (1926–2010). Bulletin of the American Astronomical Society, 42.Link (This obituary and tribute to Allan Sandage highlights his pioneering contributions to observational cosmology and his evolving spiritual outlook on life and the universe.)
30. Barrow, J. D., & Tipler, F. J. (1988). The anthropic cosmological principle. Oxford University Press. Link. (This book explores the anthropic principle and the fine-tuning of the universe for intelligent life, discussing various cosmological parameters and their implications.)
31. Sahni, V. (2002). The Case for a Positive Lambda-Term. Link. (This article discusses the role of the cosmological constant (Lambda-term) in the context of the Hubble parameter, deceleration parameter, and the age of the universe.)
32. Alhamzawi, A., & Gaidi, G. (2023). Impact of a newly parametrized deceleration parameter on the accelerating universe and the reconstruction of f(Q) non-metric gravity models. European Physical Journal C, 83(4), 356. Link. (This paper investigates the impact of a newly parametrized deceleration parameter on the accelerating universe and the reconstruction of f(Q) non-metric gravity models.)
33. Earman, J. (2020). Cosmology. Stanford Encyclopedia of Philosophy. Link. (This entry from the Stanford Encyclopedia of Philosophy provides an overview of cosmology, including discussions on the origin, evolution, and ultimate fate of the universe.)
34. Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Link. (This paper presents the cosmological parameter results from the final full-mission Planck measurements of the cosmic microwave background anisotropies, including constraints on the standard Lambda-CDM cosmological model.)
35. Tegmark, M., et al. (2006). Cosmological parameters from SDSS and WMAP. Physical Review D, 74(12), 123507. Link (This paper presents constraints on key cosmological parameters, including the matter density, dark energy density, and spatial curvature, derived from the combined analysis of data from the Sloan Digital Sky Survey (SDSS) and the Wilkinson Microwave Anisotropy Probe (WMAP).)
5
Freeman Dyson (1979): The more I examine the universe and study the details of its architecture, the more evidence I find that the universe in some sense must have known that we were coming Link
The building blocks of matter
Matter is made up of atoms, which are the basic units of chemical elements. Atoms themselves consist of even smaller particles called subatomic particles. The three fundamental subatomic particles that make up atoms are:
Protons: Protons are positively charged particles found in the nucleus of an atom. They have a relative mass of 1 atomic mass unit (u). Neutrons: Neutrons are neutral particles, having no electrical charge, also found in the nucleus of an atom. They have a similar mass to protons, around 1 u. Electrons: Electrons are negatively charged particles that orbit the nucleus of an atom. They are extremely small, with a mass of only about 1/1836 u. The number of protons in an atom's nucleus defines what element it is, while the number of protons and neutrons determines the isotope. The number of orbiting electrons is typically equal to the number of protons, making the atom electrically neutral. These subatomic particles are held together by fundamental forces: The strong nuclear force binds protons and neutrons together in the nucleus. The electromagnetic force governs the attraction between the positive nucleus and negative electrons. Further, these subatomic particles are believed to be made up of even smaller, more fundamental particles called quarks and leptons, governed by quantum physics.
What is matter made of?
The enduring stability of elements is a fundamental prerequisite for the existence of life and the opportunity for mankind to witness the universe. This requirement underscores the necessity for certain conditions that ensure matter's stability, conditions that persist even today. While this might seem self-evident given our daily interactions with stable materials like rocks, water, and various man-made objects, the underlying scientific principles are far from straightforward. The theory of quantum mechanics, developed in the 1920s, provided the framework to understand atomic structures composed of electron-filled atomic shells surrounding nuclei of protons and neutrons. However, it wasn't until the late 1960s that Freeman J. Dyson and A. Lenard made significant strides in addressing the issue of matter's stability through their groundbreaking research. Coulomb forces, responsible for the electrical attraction and repulsion between charges, play a crucial role in this stability. These forces decrease proportionally with the square of the distance between charges, akin to gravitational forces. An illustrative thought experiment involving two opposite charges demonstrates that as they move closer, the force of attraction intensifies until a critical point is reached. This raises the question: how do atomic structures maintain their integrity without collapsing into a singularity, especially considering atoms like hydrogen, which consist of a proton and an electron in close proximity?
This dilemma was articulated by J.H. Jeans even before the quantum mechanics era, highlighting the potential for infinite attraction at zero distance between charges, which could theoretically lead to the collapse of matter. However, quantum mechanics, with contributions from pioneers like Erwin Schrödinger and Wolfgang Pauli, clarified this issue. The uncertainty principle, in particular, elucidates why atoms do not implode. It dictates that the closer an electron's orbit to the nucleus, the greater its orbital velocity, thereby establishing a minimum orbital radius. This principle explains why atoms are predominantly composed of empty space, with the electron's minimum orbit being vastly larger than the nucleus's diameter, thereby preventing the collapse of atoms and ensuring the stability and expansiveness of matter in the universe. The work of Freeman J. Dyson and A. Lenard in 1967 underscored the critical role of the Pauli principle in maintaining the structural integrity of matter. Their research demonstrated that in the absence of this principle, the electromagnetic force would cause atoms and even bulk matter to collapse into a highly condensed phase, with potentially catastrophic energy releases upon the interaction of macroscopic objects, comparable to nuclear explosions. In our observable reality, matter is predominantly composed of atoms, which, when closely examined, reveal a vast expanse of what appears to be empty space. If one were to scale an atom to the size of a stadium, its nucleus would be no larger than a fly at the center, with electrons resembling minuscule insects circling the immense structure. This analogy illustrates the notion that what we perceive as solid and tangible is, on a subatomic level, almost entirely empty space. This "space," once thought to be a void, is now understood through the lens of quantum physics to be teeming with energy. Known by various names—quantum foam, ether, the plenum, vacuum fluctuations, or the zero-point field—this energy vibrates at an incredibly high frequency, suggesting that the universe is vibrant of energy rather than emptiness.
The stability of any bound system, from atomic particles to celestial bodies, hinges on the equilibrium between forces of attraction that bind and repulsive forces that prevent collapse. The structure of matter at various scales is influenced by how these forces interact over distance. Observationally, the largest cosmic structures are shaped by gravity, the weakest force, while the realm of elementary particles is governed by the strong nuclear force, the most potent of all. This observable hierarchy of forces is logical when considering that stronger forces will naturally overpower weaker ones, drawing objects closer and forming more tightly bound systems. The hierarchy is evident in the way stronger forces can break bonds formed by weaker ones, pulling objects into closer proximity and resulting in smaller, more compact structures. The range and nature of these forces also play a role in this hierarchical structure. Given enough time, particles will interact and mix, with attraction occurring regardless of whether the forces are unipolar, like gravity, or bipolar, like electromagnetism. The universe's apparent lack of a net charge ensures that opposite charges attract, leading to the formation of bound systems.
Interestingly, the strongest forces operate within short ranges, precisely where they are most effective in binding particles together. As a result, stronger forces lead to the release of more binding energy during the formation process, simultaneously increasing the system's internal kinetic energy. In systems bound by weaker forces, the total mass closely approximates the sum of the constituent masses. However, in tightly bound systems, the significant internal kinetic and binding energies must be accounted for, as exemplified by the phenomenon of mass defect in atomic nuclei. Progressing through the hierarchy from weaker to stronger forces reveals that each deeper level of binding, governed by a stronger force and shorter range, has more binding energy. This energy, once released, contributes to the system's internal kinetic energy, which accumulates with each level. Eventually, the kinetic energy could match the system's mass, reaching a limit where no additional binding is possible, necessitating a transition from discrete particles to a continuous energy field. The exact point of this transition is complex to pinpoint but understanding it at an order-of-magnitude level provides valuable insights. The formation of bound systems, such as the hydrogen atom, involves the reduction of potential energy as particles are brought together, necessitating the presence of a third entity to conserve energy, momentum, and angular momentum. Analyzing the energy dynamics of the hydrogen atom, deuteron, and proton helps elucidate the interplay of forces and energy in the binding process. The formation of a hydrogen atom from a proton and an electron, for instance, showcases how kinetic energy is gained at the expense of potential energy, leading to the creation of a bound state accompanied by the emission of electromagnetic radiation, illustrating the complex interplay of forces that govern the structure and stability of matter across the universe.

In the realm of contemporary physics, the stability of matter across varying scales is fundamentally a consequence of the interplay between forces acting upon bound entities, whether they be objects, particles, or granules. The proton, recognized as the smallest stable particle, exemplifies this principle. Its stability is thought to arise from a dynamic equilibrium where forces are balanced within a perpetual flow of energy, conceptualized as a loop or knot moving at the speed of light. This internal energy, which participates in electromagnetic interactions, suggests that matter might be more accurately described by some form of topological electromagnetism, potentially challenging or expanding our current understanding of space-time. Echoing this perspective, Further delving into this paradigm, modern physics increasingly views the material universe as a manifestation of wave phenomena. These waves are categorized into two types: localized waves, which we perceive as matter, and free-traveling waves, known as radiation or light. The transformation of matter, such as in annihilation events, is understood as the release of contained wave-energy, allowing it to propagate freely. This wave-centric view of the universe encapsulates its essence in a poetic simplicity, suggesting that the genesis of everything could be encapsulated in the notion of light being called into existence, resonating with the ancient scriptural idea of creation through divine command.
Atoms
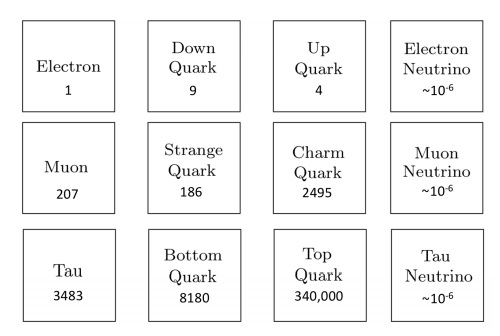
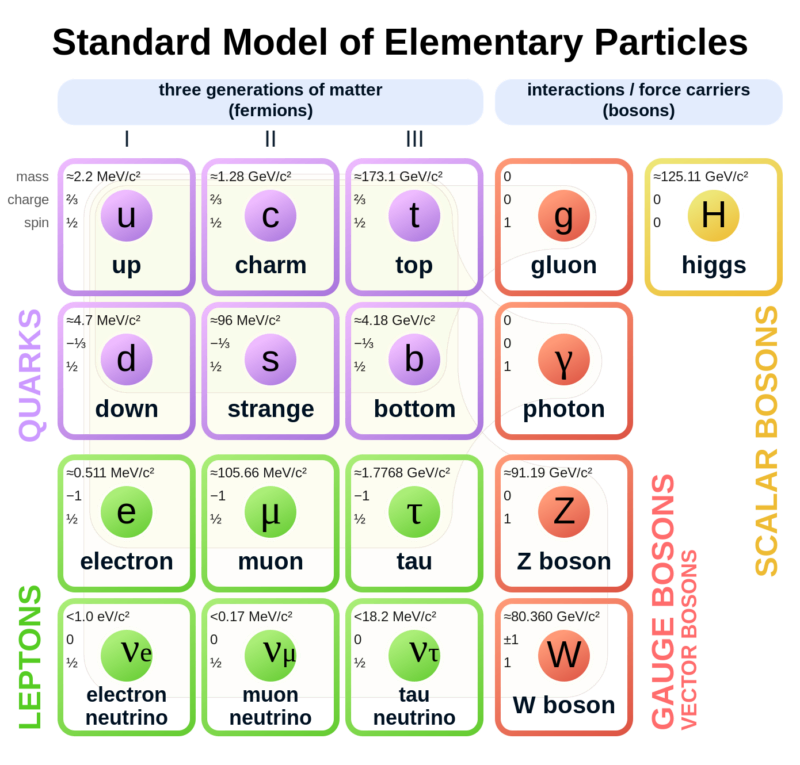
Atoms are indeed the fundamental units that compose all matter, akin to the letters forming the basis of language. Much like how various combinations of letters create diverse words, atoms combine to form molecules, which in turn construct the myriad substances we encounter in our surroundings. From the biological structures of our bodies and the flora and fauna around us to the geological formations of rocks and minerals that make up our planet, the diversity of materials stems from the intricate arrangements of atoms and molecules. Initially, our understanding of matter centered around a few key subatomic particles: protons, neutrons, and electrons. These particles, which constitute the nucleus and orbitals of atoms, provided the foundation for early atomic theory. However, with advancements in particle physics, particularly through the utilization of particle accelerators, the list of known subatomic particles expanded exponentially. This expansion culminated in what physicists aptly described as a "particle zoo" by the late 1950s, reflecting the complex array of fundamental constituents of matter. The elucidation of this seemingly chaotic landscape came with the introduction of the quark model in 1964 by Murray Gell-Mann and George Zweig. This model proposed that many particles observed in the "zoo" are not elementary themselves but are composed of smaller, truly elementary particles known as quarks and leptons. The quark model identifies six types of quarks—up, down, charm, strange, top, and bottom—which combine in various configurations to form other particles, such as protons and neutrons. For instance, a proton comprises two up quarks and one down quark, while a neutron consists of one up quark and two down quarks. This elegant framework significantly simplified our understanding of matter's basic constituents, reducing the apparent complexity of the particle zoo.
Beyond quarks and leptons, scientists propose the existence of other particles that mediate fundamental forces. One such particle is the photon, which plays a crucial role in electromagnetic interactions as a massless carrier of electromagnetic energy. The subatomic realm is further delineated by five key players: protons, neutrons, electrons, neutrinos, and positrons, each characterized by its mass, electrical charge, and spin. These particles, despite their minuscule size, underpin the physical properties and behaviors of matter. Atoms, as the fundamental units of chemical elements, exhibit remarkable diversity despite their structural simplicity. The periodic table encompasses around 100 chemical elements, each distinguished by a unique atomic number, denoting the number of protons in the nucleus. From hydrogen, the simplest element with an atomic number of 1, to uranium, the heaviest naturally occurring element with an atomic number of 92, these elements form the basis of all known matter. Each element's distinctive properties dictate its behavior in chemical reactions, analogous to how the position of a letter in the alphabet determines its function in various words. Within atoms, a delicate balance of subatomic particles—electrons, protons, and neutrons—maintains stability and order. Neutrons play a critical role in stabilizing atoms; without the correct number of neutrons, the equilibrium between electrons and protons is disrupted, leading to instability. Removal of a neutral neutron can destabilize an atom, triggering disintegration through processes such as fission, which releases vast amounts of energy. The nucleus, despite its small size relative to the atom, accounts for over 99.9% of an atom's total mass, underscoring its pivotal role in determining an atom's properties. From simple compounds like salt to complex biomolecules such as DNA, the structural variety of molecules mirrors the rich complexity of the natural world. Yet, this complexity emerges from the structured interplay of neutrons, protons, and electrons within atoms, governed by the principles of atomic physics. Thus, while molecules embody the vast spectrum of chemical phenomena, it is the underlying organization of atoms that forms the bedrock of molecular complexity.

The Proton
In physics, the proton has a mass roughly 1836 times that of an electron. This stark mass disparity is not merely a numerical curiosity but a fundamental pillar that underpins the structural dynamics of atoms. The lighter electrons orbit the nucleus with agility, made possible by their comparative lightness. A reversal of this mass relationship would disrupt the atomic ballet, altering the very essence of matter and its interactions. The universe's architectural finesse extends to the mass balance among protons, neutrons, and electrons. Neutrons, slightly heavier than the sum of a proton and an electron, can decay into these lighter particles, accompanied by a neutrino. This transformation is a linchpin in the universe's elemental diversity. A universe where neutrons matched the combined mass of protons and electrons would have stifled hydrogen's abundance, crucial for star formation. Conversely, overly heavy neutrons would precipitate rapid decay, possibly confining the cosmic inventory to the simplest elements.
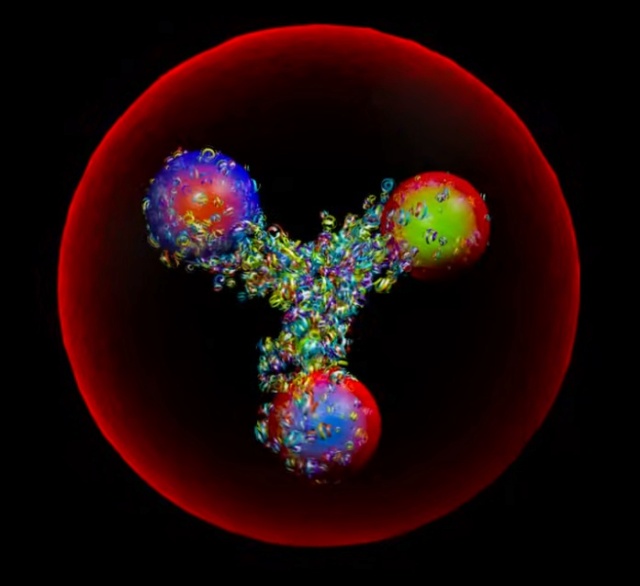
The image represents an artistic visualization or model of a proton. The large red sphere depicts the overall structure of the proton. The vibrant, fractal-like formations inside the sphere represent the internal composition of the proton, with the different colored clusters potentially symbolizing the constituent quarks and gluons that make up this subatomic particle. This rendition captures the proton's complex, energetic inner dynamics and structure within the boundaries of its outer sphere or field. While not a scientifically accurate model, it provides a visually striking and abstract interpretation of one of the fundamental particles of matter.
Electrons, despite their minuscule mass, engage with a trio of the universe's fundamental forces: gravity, electromagnetism, and the weak nuclear force. This interplay shapes electron behavior within atoms and their broader cosmic role, weaving into the fabric of physical laws that govern the universe. The enduring stability of protons, contrasting sharply with the transient nature of neutrons, secures a bedrock for existence. Protons' resilience ensures the continuity of hydrogen, the simplest atom, foundational to water, organic molecules, and stars like our Sun. The stability of protons versus the instability of neutrons hinges on a slight mass difference, a quirk of nature where the neutron's extra mass—and thus energy—enables its decay, releasing energy. This balance is delicate; a heavier proton would spell catastrophe, obliterating hydrogen and precluding life as we know it. This critical mass interplay traces back to the quarks within protons and neutrons. Protons abound with lighter u quarks, while neutrons are rich in heavier d quarks. The mystery of why u quarks are lighter remains unsolved, yet this quirk is a cornerstone for life's potential in our universe. Neutrons, despite their propensity for decay in isolation, find stability within the nucleus, shielded by the quantum effect known as Fermi energy. This stability within the nucleus ensures that neutrons' fleeting nature does not undermine the integrity of atoms, preserving the complex structure of elements beyond hydrogen. The cosmic ballet of particles, from the stability of protons to the orchestrated decay of neutrons, reflects a universe finely tuned for complexity and life. The subtle interplay of masses, forces, and quantum effects narrates a story of balance and possibility, underpinning the vast expanse of the cosmos and the emergence of life within it.
If a proton were scaled up to the size of a grain of sand and kept its properties, including density, remained the same, it would have a weight of approximately roughly 389 million kilograms! This is equivalent to the weight of many large cruise ships combined. So, the weight of the scaled-up proton would be approximately metric tons or 389,000 metric tons. Eiffel Tower: The Eiffel Tower in Paris weighs approximately 10,100 metric tons. The proton's weight in this scenario would be equivalent to nearly 39 Eiffel Towers. The mass of a proton arises primarily from the strong nuclear force. The majority of the proton's mass doesn't come from the rest masses of these quarks but from the binding energy of these particles inside the proton, as per the principle of E=mc2. If we take just the strong nuclear force, it is adjusted by one part in 10^40 (or 10,000 billion billion billion billion). If we scaled up the proton to 389,000 metric tons, based on the fine-tuning parameter of one part in one part in 10^40, the weight could change by approximately 3.89×10^24 milligrams. approximately 2.57×10^26 milligram units would fit into one gram. If our universe had protons with a slightly different mass, life might not be possible at all.
The six defining characteristics and principles of the strong nuclear force are:
Quantum Chromodynamics (QCD): Quantum Chromodynamics is the theory that describes the strong nuclear force. It is a fundamental theory of particle physics that explains how the strong force operates between particles called quarks and gluons.
Color Charge: Quarks, which are the elementary particles that make up protons and neutrons, carry a property called color charge. Color charge is an attribute similar to electric charge but associated with the strong force. Quarks can have three different colors: red, green, and blue.
Confinement: Confinement is a property of the strong force that explains why quarks are never found alone in isolation. In nature, quarks are always bound together in groups, forming composite particles such as protons and neutrons. The strong force becomes stronger as quarks are pulled apart, making it impossible to separate them completely.
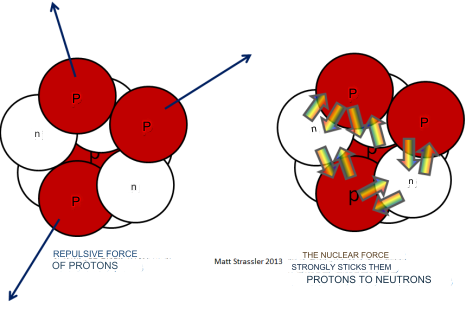
Binding Nucleons (or Residual Strong Force): The strong force is responsible for binding nucleons (protons and neutrons) together within an atomic nucleus. This attraction between nucleons is often referred to as the residual strong force or nuclear force.
Gluons: Gluons are the force-carrying particles of the strong nuclear force. They mediate the interactions between quarks, transmitting the strong force between them. Gluons themselves carry color charge and can interact with other gluons.
Asymptotic Freedom: Asymptotic freedom is a property of the strong force that was discovered through the theory of Quantum Chromodynamics (QCD). It states that at very high energy levels or short distances, the strong force weakens. This means that the interactions between quarks become weaker as they get closer together, allowing for more freedom of movement. Asymptotic freedom is an important aspect of QCD and helps explain the behavior of quarks and gluons at extreme conditions.
Within the context of our current theories, they aren't derived from more basic principles or mechanisms. They are foundational elements of our theoretical understanding of the universe at the quantum level. There are no scientific reasons to declare them "necessary" in the sense that they had to have the values they do. What's truly fascinating and somewhat mysterious for physicists is why these constants have the particular values they do.
Mathematical Elegance and Beauty: Many of the fundamental laws of physics can be expressed in extremely concise mathematical forms. For instance, Maxwell's equations, which describe all classical electromagnetic phenomena, or Einstein's E=mc2, which captures the relationship between energy and mass, are marvelously simple and compact.

The physicist Eugene Wigner wrote a famous paper titled "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," in which he pondered why mathematics, a product of human thought, is so adept at describing the physical world. While Wigner didn't argue for a creator, we can use this observation as evidence that the universe is constructed upon a rational and logical foundation, indicative of a Designer. Historically, scientists, from Kepler to Einstein, have often been guided by a sense of beauty and elegance in their search for truth. They believed that the most beautiful equations were more likely to be true. This intrinsic beauty is not merely a happy coincidence but points towards a universe with purpose and design. The very fact we can describe the universe mathematically, and that it follows logical and rational laws, suggests a mind-like quality to the universe. If the universe follows logic and reason, it seems rational to infer that most probably it is the product of Logic and Reason by a conscious, intelligent creator. The laws of physics are not just elegant; they're universally so. Gravity works the same way on Earth as it does in a galaxy billions of light-years away. Universality further strengthens the idea of a single, coherent design.
Do protons vibrate?
Protons, which are subatomic particles found in the nucleus of an atom, do not exhibit classical vibrations like macroscopic objects. However, they do possess a certain amount of internal motion due to their quantum nature. According to quantum mechanics, particles like protons are described by wave functions, which determine their behavior and properties. The wave function of a proton includes information about its position, momentum, and other characteristics. This wave function can undergo quantum fluctuations, causing the proton to exhibit a form of internal motion or "vibration" on a quantum level. These quantum fluctuations imply that the position of a proton is not precisely determined but rather exists as a probability distribution. The proton's position and momentum are subject to the Heisenberg uncertainty principle, which states that there is an inherent limit to the precision with which certain pairs of physical properties can be known simultaneously. However, it's important to note that these quantum fluctuations are different from the macroscopic vibrations we typically associate with objects. They are inherent to the nature of particles on a microscopic scale and are governed by the laws of quantum mechanics. So, while protons do not vibrate in a classical sense, they do exhibit internal motion and quantum fluctuations as described by their wave functions. These quantum effects are fundamental aspects of the behavior of particles at the subatomic level.
The Neutron
The neutron is a subatomic particle with no electric charge, found in the nucleus of an atom alongside protons. Neutrons and protons, collectively known as nucleons, are close in mass, yet distinct enough to enable the intricate balance required for the universe's complex chemistry. Neutrons are slightly heavier than protons, a feature that is crucial for the stability of most atoms. If neutrons were significantly lighter than protons, they would decay into protons more readily, making it difficult for atoms to maintain the neutron-proton balance necessary for stability. Conversely, if neutrons were much heavier, they would convert to protons too quickly, again disrupting the delicate balance required for complex atoms to exist. The stability of an atom’s nucleus depends on the fine balance between the attractive nuclear force and the repulsive electromagnetic force between protons. Neutrons play a vital role in this balance by adding to the attractive force without increasing the electromagnetic repulsion, as they carry no charge. This allows the nucleus to have more protons, which would otherwise repel each other due to their positive charge. This delicate balance has far-reaching implications for the universe and the emergence of life. For instance:
Nuclear Fusion in Stars: The mass difference between protons and neutrons is crucial for the process of nuclear fusion in stars, where hydrogen atoms fuse to form helium, releasing energy in the process. This energy is the fundamental source of heat and light that makes life possible on planets like Earth.
Synthesis of Heavier Elements: After the initial fusion processes in stars, the presence of neutrons allows for the synthesis of heavier elements. Neutrons can be captured by nuclei, which then undergo beta decay (where a neutron is converted into a proton), leading to the formation of new elements. This process is essential for the creation of the rich array of elements that are the building blocks of planets, and ultimately, life.
Chemical Reactivity: The number of neutrons affects the isotopic nature of elements, influencing their stability and chemistry. Some isotopes are radioactive and can provide a source of heat, such as that driving geothermal processes on Earth, which have played a role in life's evolution.
Stable Atoms: The existence of stable isotopes for the biochemically critical elements such as carbon, nitrogen, oxygen, and phosphorus is a direct consequence of the neutron-proton mass ratio. Without stable isotopes, the chemical reactions necessary for life would not proceed in the same way.
In the cosmic balance for life to flourish, the neutron's role is subtle yet powerful. Its finely tuned relationship with the proton—manifested in the delicate dance within the atomic nucleus—has allowed the universe to be a place where complexity can emerge and life can develop. This fine-tuning of the properties of the neutron, in concert with the proton and the forces governing their interactions, is one of the many factors contributing to the habitability of the universe.
The Electron
Electrons, those infinitesimal carriers of negative charge, are central to the physical universe. Discovered in the 1890s, they are considered fundamental particles, their existence signifying the subatomic complexity beyond the once-assumed indivisible atom. The term "atom" itself, derived from the Greek for "indivisible," became a misnomer with the electron's discovery, heralding a new understanding of matter's divisible, complex nature. By the mid-20th century, thanks to quantum mechanics, our grasp of atomic structures and electron behavior had deepened, underscoring electrons' role as uniform, indistinguishable pillars of matter. In everyday life, electrons are omnipresent. They emit the photons that make up light, transmit the sounds we hear, participate in the chemical reactions responsible for taste and smell, and provide the resistance we feel when touching objects. In plasma globes and lightning bolts, their paths are illuminated, tracing luminous arcs through space. The chemical identities of elements, the compounds they form, and their reactivity all hinge on electron properties. Any change in electron mass or charge would recalibrate chemistry entirely. Heavier electrons would condense atoms, demanding more energetic bonds, potentially nullifying chemical bonding. Excessively light electrons, conversely, would weaken bonds, destabilizing vital molecules like proteins and DNA, and turning benign radiation into harmful energy, capable of damaging our very genetic code.
The precise mass of electrons, their comparative lightness to protons and neutrons, is no mere happenstance—it is a prerequisite for the rich chemistry that supports life. Stephen Hawking, in "A Brief History of Time," contemplates the fundamental numbers that govern scientific laws, including the electron's charge and its mass ratio to protons. These constants appear finely tuned, fostering a universe where stars can burn and life can emerge. The proton-neutron mass relationship also plays a crucial part. They are nearly equal in mass yet distinct enough to prevent universal instability. The slightly greater mass of neutrons than protons ensures the balance necessary for the complex atomic arrangements that give rise to life. Adding to the fundamental nature of electrons, Niels Bohr's early 20th-century quantization rule stipulates that electrons occupy specific orbits, preserving atomic stability and the diversity of elements. And the Pauli Exclusion Principle, as noted by physicist Freeman Dyson, dictates that no two fermions (particles with half-integer spins like electrons) share the same quantum state, allowing only two electrons per orbital and preventing a collapse into a chemically inert universe. These laws—the quantization of electron orbits and the Pauli Exclusion Principle—form the bedrock of the complex chemistry that underpins life. Without them, our universe would be a vastly different, likely lifeless, expanse. Together, they compose a symphony of physical principles that not only allow the existence of life but also enable the myriad forms it takes.
The diverse array of atomic bonds, all rooted in electron interactions, is essential for the formation of complex matter. Without these bonds, the universe would be devoid of molecules, liquids, and solids, consisting solely of monatomic gases. Five main types of atomic bonds exist, and their strengths are influenced by the specific elements and distances between atoms involved. The fine-tuning for atomic bonds involves precise physical constants and forces in the universe, such as electromagnetic force and the specific properties of electrons. These elements must be finely balanced for atoms to interact and form stable bonds, enabling the complexity of matter. Chemical reactions hinge on the formation and disruption of chemical bonds, which essentially involve electron interactions. Without the capability of electrons to create breakable bonds, chemical reactions wouldn't occur. These reactions, which can be seen as electron transfers involving energy shifts, underpin processes like digestion, photosynthesis, and combustion, extending to industrial applications in making glues, paints, and batteries. In photosynthesis, specifically, electrons energized by light photons are transferred between molecules, facilitating ATP production in chloroplasts.
Electricity involves electron movement through conductors, facilitating energy transfer between locations, like from a battery to a light bulb. Light is generated when charged particles like electrons accelerate, emitting electromagnetic radiation without losing energy in atomic orbits.
Getting the Right Electrons
Hugh Ross (2001) Not only must the universe be fine-tuned to get enough nucleons, but also a precise number of electrons must exist. Unless the number of electrons is equivalent to the number of protons to an accuracy of one part in 10^37, or better, electromagnetic forces in the universe would have so overcome gravitational forces that galaxies, stars, and planets never would have formed. One part in 10^37 is such an incredibly sensitive balance that it is hard to visualize. The following analogy might help:
Cover the entire North American continent in dimes all the way up to the moon, a height of about 239,000 miles. (In comparison, the money to pay for the U.S. federal government debt would cover one square mile less than two feet deep with dimes.) Next, pile dimes from here to the moon on a billion other continents the same size as North America. Paint one dime red and mix it into the billion piles of dimes. Blindfold a friend and ask him to pick out one dime. The odds that he will pick the red dime are one in 10^37. And this is only one of the parameters that is so delicately balanced to allow life to form.
At whatever level we examine the building blocks of life‹electrons, nucleons, atoms, or molecules‹the physics of the universe must be very meticulously fine-tuned. The universe must be exactingly constructed to create the necessary electrons. It must be exquisitely crafted to produce the protons and neutrons required. It must be carefully fabricated to obtain the needed atoms. Unless it is skillfully fashioned, the atoms will not be able to assemble into complex enough molecules. Such precise balancing of all these factors is truly beyond our ability to comprehend. 8
Subatomic particles
Following is a list of subatomic particles with short descriptions:
Quarks
Up Quark (u): One of the fundamental constituents of matter, with a charge of +2/3 e.
Down Quark (d): One of the fundamental constituents of matter, with a charge of -1/3 e.
Strange Quark (s): A heavier quark with a charge of -1/3 e, part of the second generation of matter particles.
Charm Quark (c): A heavier quark with a charge of +2/3 e, part of the second generation of matter particles.
Bottom Quark (b): A very heavy quark with a charge of -1/3 e, part of the third generation of matter particles.
Top Quark (t): The heaviest known quark, with a charge of +2/3 e, part of the third generation of matter particles.
Leptons
Electron (e): A stable, lightweight lepton with a charge of -1 e, part of the first generation of matter particles.
Electron Neutrino (νe): A neutrally charged, lightweight lepton associated with the electron, part of the first generation of matter particles.
Muon (μ): An unstable, heavier lepton with a charge of -1 e, part of the second generation of matter particles.
Muon Neutrino (νμ): A neutrally charged lepton associated with the muon, part of the second generation of matter particles.
Tau (τ): An unstable, very heavy lepton with a charge of -1 e, part of the third generation of matter particles.
Tau Neutrino (ντ): A neutrally charged lepton associated with the tau, part of the third generation of matter particles.
Gauge Bosons
Photon (γ): The massless carrier of the electromagnetic force.
W Boson (W+, W-): Massive carriers of the weak nuclear force, responsible for mediating certain types of radioactive decay.
Z Boson (Z): A massive, neutrally charged carrier of the weak nuclear force.
Gluon (g):The massless carrier of the strong nuclear force, responsible for binding quarks together within hadrons.
Higgs Boson
Higgs Boson (H): A massive particle responsible for giving other particles their mass through the Higgs mechanism.
Other Particles
Pions (π+, π-, π0):_ Unstable hadrons composed of a quark and an antiquark, involved in the strong nuclear force.
Kaons (K+, K-, K0, K̄0):_ Unstable hadrons composed of a quark and an antiquark, involved in the weak and strong nuclear forces.
Mesons: Unstable particles composed of a quark and an antiquark, involved in the strong and/or weak nuclear forces.
Baryons: Particles composed of three quarks, including protons and neutrons.
Antiparticles: Corresponding antimatter counterparts to each particle, with the same mass but opposite charge.
These particles are the fundamental building blocks of matter and the carriers of the fundamental forces in nature. Their properties and interactions are studied in particle physics to understand the nature of matter, energy, and the universe at the most fundamental level.
Element Production in the Early Universe
Let's examine the steps involved in element production during the Big Bang. In the initial fireball, matter existed primarily in the form of neutrons. Once released from their extreme confinement, neutrons underwent spontaneous radioactive decay into protons and electrons, with half of the neutrons decaying every 10.2 minutes – known as the half-life of this decay process. (For example, after three half-lives, only one-eighth of the original atoms remain.)
During those crucial minutes of stability, many neutrons collided with protons to form deuterium (2H), an isotope of hydrogen consisting of one proton and one neutron. Other collisions led to the creation of nuclei with masses 3 and 4 (helium atoms). At this point, a remarkable aspect of nuclear stability becomes apparent: there exist no stable nuclei with mass numbers 5 or 8. A helium nucleus colliding with the abundant protons or neutrons would not produce a reaction. Likewise, two helium atoms colliding would also yield no result. Instead, only rare "three-body" collisions could overcome this mass gap, producing nuclei of masses 6, 7, or 9. For example, a proton and a neutron would have to collide simultaneously with a 4He nucleus to form 6Li. However, such "three-ball" collisions were far less frequent than "two-ball" collisions in the expanding gas cloud. As a result, the number of nuclei formed heavier than 4He was insignificant. Thus, at the end of the initial cosmic epoch, the universe's matter consisted almost entirely of the elements hydrogen and helium, with only trace amounts of the next three elements – lithium (Li), beryllium (Be), and boron (B). Further nucleosynthesis awaited the formation of galaxies and the birth of stars within these galaxies.
Physicists have modeled the collisions that would have occurred during this primordial cosmic phase. They found that for every ten hydrogen atoms, there would have been one helium atom. This ratio matches the fraction of helium observed in young stars throughout the universe, providing the third line of evidence for the Big Bang hypothesis.
Stellar Nucleosynthesis
Stars are internally hot for the same reason that brake shoes on a stopping car become hot. When a moving vehicle is brought to a stop, the kinetic energy associated with its motion is converted to heat in the brake linings. During the gravitational collapse of a gas cloud, the gravitational potential energy is likewise transformed into heat. The amount of heat produced is so vast, and the insulation provided by the enshrouding envelope of gas so effective, that the core of the protostar becomes hot enough to ignite nuclear fusion. For nuclei in a star to undergo fusion reactions, they must collide and come into direct contact. To achieve this, they must fly at one another at extremely high velocities, overcoming the electrical repulsion exerted by the positively charged protons. It is akin to trying to throw a ping-pong ball into a fan – a very high velocity is required to prevent the ball from being blown back. The hotter atoms are, the faster they move. Temperature is a scale that quantifies this molecular motion. Touching a hot stove causes the molecules in the skin of your finger to move so rapidly that the chemical bonds holding them in place are broken, resulting in a burn. For two protons to collide requires velocities equivalent to a temperature of about 60,000,000°C. Through a series of collisions, four protons (and two electrons) can combine to produce a helium nucleus. This helium nucleus contains two of the original protons and two neutrons that were formed through the merger of protons with electrons (for each proton in a star, there must be one electron). As first recognized by Einstein, for nuclear fusion to occur, there must be a release of energy, and this energy release results in a reduction of mass. This lost mass reappears as heat. Indeed, the weight of a helium atom is slightly less than that of four hydrogen atoms, and this mass deficit is converted to heat when the helium atom is synthesized in a star's core. The amount of heat obtained in this process is phenomenal. The proponents of fusion power are quick to point out this fact. Once a protostar's nuclear fire is ignited, its collapse stems by the outward pressure created by the escape of the heat generated. The star stabilizes in size and burns smoothly for an extremely long period. For example, our Sun has burned for thousands of years and does not need to exhaust its hydrogen fuel for several more billion years. Most of the stars we observe are emitting light created by the heat from hydrogen-burning nuclear furnaces. Thus, one could say that stars are continuing the work begun during the first epoch of the universe's history; they are slowly converting the remaining hydrogen into helium. Our Sun is small enough that hydrogen burning can sustain it for billions of years. Since helium nuclei have two protons, the force of electrical repulsion between them is four times stronger than the repulsion between two hydrogen nuclei. At the temperatures of hydrogen fusion, the nuclear velocities are insufficient to overcome this electrostatic barrier. For this reason, fusion of helium atoms does not occur in small stars like our Sun.
Within the core of a large star, however, the gravitational attraction is more intense, and to counter it, the hydrogen fuel is converted to helium relatively rapidly. These so-called red giants exhaust their hydrogen supply in about a million years. When the core of a red giant becomes depleted of hydrogen, the nuclear fire dims, and the star loses its ability to resist the inward pull of gravity. It once again begins to collapse. The energy released by this renewed collapse causes the core temperature to rise and the pressure to increase. The higher temperatures reach the ignition threshold required for helium fusion. Then, helium nuclei begin to fuse, forming carbon nuclei (three 4He nuclei merge to form one 12C nucleus). The mass of the carbon atom is less than that of the three helium atoms from which it was formed. This mass deficit appears as heat. The heat from the rekindled nuclear fire stems the star's collapse, and its size once again stabilizes. In massive stars, this cycle of fuel depletion, renewed collapse, core temperature rise, and ignition of a less fusible nuclear fuel is repeated several times. A carbon nucleus can fuse with a helium nucleus to form oxygen, or two carbon nuclei can merge to form magnesium, and so forth. Each merger leads to a small loss of mass and the corresponding production of heat. This entire process can continue as long as fusion produces lighter nuclei, resulting in a mass decrease and heat production. The extra heat is needed to prevent the star from collapsing further and to maintain a stable state where outward heat pressure balances inward gravitational contraction. The maximum mass that can be created by this process is the isotope 56Fe. Above this mass, the merger of nuclei does not lead to a mass decrease; instead, heat must be added to nuclei for them to fuse. That is, since mass and energy are related by E = mc^2, the mass of nuclei heavier than iron proves to be slightly larger than the mass of the nuclei that are merged to form them. These reactions are heat sinks rather than heat sources and therefore cannot stem the gravitational collapse of the star. For this reason, the nuclear furnaces of stars can produce only elements ranging from helium to iron. It should be noted that included in this range are the elements carbon, nitrogen, oxygen, magnesium, and silicon.
We are then left with two problems. First, there are many elements more massive than 56Fe. How can these be produced? Second, synthesizing elements in stellar interiors is not useful for planet-building if the elements remain trapped inside. There must be some distribution mechanism that allows these elements to become broadly dispersed throughout the universe. We know this dispersal must occur not only because of the compositions of the planets but also due to the composition of the Sun itself. The solar spectrum shows that all elements exist in the Sun, indicating that the materials from which it formed must have included all the elements and not just hydrogen and helium. Before discussing the solution to these two problems, let us briefly consider the fate of smaller stars like our Sun. When the core of our Sun runs out of hydrogen fuel several billion years from now, it will resume its collapse. However, our Sun is just barely massive enough to generate the temperature necessary to start a helium-burning phase. After exhausting its core helium, it will collapse into a very dense object that will cool slowly until it emits only a dull glow. Such an object is referred to as a white dwarf star.
Last edited by Otangelo on Fri May 31, 2024 10:07 am; edited 21 times in total