The enduring stability of elements is a fundamental prerequisite for the existence of life and the opportunity for mankind to witness the universe. This requirement underscores the necessity for certain conditions that ensure matter's stability, conditions that persist even today. While this might seem self-evident given our daily interactions with stable materials like rocks, water, and various man-made objects, the underlying scientific principles are far from straightforward. The theory of quantum mechanics, developed in the 1920s, provided the framework to understand atomic structures composed of electron-filled atomic shells surrounding nuclei of protons and neutrons. However, it wasn't until the late 1960s that Freeman J. Dyson and A. Lenard made significant strides in addressing the issue of matter's stability through their groundbreaking research. Coulomb forces, responsible for the electrical attraction and repulsion between charges, play a crucial role in this stability. These forces decrease proportionally with the square of the distance between charges, akin to gravitational forces. An illustrative thought experiment involving two opposite charges demonstrates that as they move closer, the force of attraction intensifies until a critical point is reached. This raises the question: how do atomic structures maintain their integrity without collapsing into a singularity, especially considering atoms like hydrogen, which consist of a proton and an electron in close proximity?
This dilemma was articulated by J.H. Jeans even before the quantum mechanics era, highlighting the potential for infinite attraction at zero distance between charges, which could theoretically lead to the collapse of matter. However, quantum mechanics, with contributions from pioneers like Erwin Schrödinger and Wolfgang Pauli, clarified this issue. The uncertainty principle, in particular, elucidates why atoms do not implode. It dictates that the closer an electron's orbit to the nucleus, the greater its orbital velocity, thereby establishing a minimum orbital radius. This principle explains why atoms are predominantly composed of empty space, with the electron's minimum orbit being vastly larger than the nucleus's diameter, thereby preventing the collapse of atoms and ensuring the stability and expansiveness of matter in the universe. The work of Freeman J. Dyson and A. Lenard in 1967 underscored the critical role of the Pauli principle in maintaining the structural integrity of matter. Their research demonstrated that in the absence of this principle, the electromagnetic force would cause atoms and even bulk matter to collapse into a highly condensed phase, with potentially catastrophic energy releases upon the interaction of macroscopic objects, comparable to nuclear explosions. In our observable reality, matter is predominantly composed of atoms, which, when closely examined, reveal a vast expanse of what appears to be empty space. If one were to scale an atom to the size of a stadium, its nucleus would be no larger than a fly at the center, with electrons resembling minuscule insects circling the immense structure. This analogy illustrates the notion that what we perceive as solid and tangible is, on a subatomic level, almost entirely empty space. This "space," once thought to be a void, is now understood through the lens of quantum physics to be teeming with energy. Known by various names—quantum foam, ether, the plenum, vacuum fluctuations, or the zero-point field—this energy vibrates at an incredibly high frequency, suggesting that the universe is vibrant of energy rather than emptiness.
The stability of any bound system, from atomic particles to celestial bodies, hinges on the equilibrium between forces of attraction that bind and repulsive forces that prevent collapse. The structure of matter at various scales is influenced by how these forces interact over distance. Observationally, the largest cosmic structures are shaped by gravity, the weakest force, while the realm of elementary particles is governed by the strong nuclear force, the most potent of all. This observable hierarchy of forces is logical when considering that stronger forces will naturally overpower weaker ones, drawing objects closer and forming more tightly bound systems. The hierarchy is evident in the way stronger forces can break bonds formed by weaker ones, pulling objects into closer proximity and resulting in smaller, more compact structures. The range and nature of these forces also play a role in this hierarchical structure. Given enough time, particles will interact and mix, with attraction occurring regardless of whether the forces are unipolar, like gravity, or bipolar, like electromagnetism. The universe's apparent lack of a net charge ensures that opposite charges attract, leading to the formation of bound systems.
Interestingly, the strongest forces operate within short ranges, precisely where they are most effective in binding particles together. As a result, stronger forces lead to the release of more binding energy during the formation process, simultaneously increasing the system's internal kinetic energy. In systems bound by weaker forces, the total mass closely approximates the sum of the constituent masses. However, in tightly bound systems, the significant internal kinetic and binding energies must be accounted for, as exemplified by the phenomenon of mass defect in atomic nuclei. Progressing through the hierarchy from weaker to stronger forces reveals that each deeper level of binding, governed by a stronger force and shorter range, has more binding energy. This energy, once released, contributes to the system's internal kinetic energy, which accumulates with each level. Eventually, the kinetic energy could match the system's mass, reaching a limit where no additional binding is possible, necessitating a transition from discrete particles to a continuous energy field. The exact point of this transition is complex to pinpoint but understanding it at an order-of-magnitude level provides valuable insights. The formation of bound systems, such as the hydrogen atom, involves the reduction of potential energy as particles are brought together, necessitating the presence of a third entity to conserve energy, momentum, and angular momentum. Analyzing the energy dynamics of the hydrogen atom, deuteron, and proton helps elucidate the interplay of forces and energy in the binding process. The formation of a hydrogen atom from a proton and an electron, for instance, showcases how kinetic energy is gained at the expense of potential energy, leading to the creation of a bound state accompanied by the emission of electromagnetic radiation, illustrating the complex interplay of forces that govern the structure and stability of matter across the universe.

In the realm of contemporary physics, the stability of matter across varying scales is fundamentally a consequence of the interplay between forces acting upon bound entities, whether they be objects, particles, or granules. The proton, recognized as the smallest stable particle, exemplifies this principle. Its stability is thought to arise from a dynamic equilibrium where forces are balanced within a perpetual flow of energy, conceptualized as a loop or knot moving at the speed of light. This internal energy, which participates in electromagnetic interactions, suggests that matter might be more accurately described by some form of topological electromagnetism, potentially challenging or expanding our current understanding of space-time. Echoing this perspective, Further delving into this paradigm, modern physics increasingly views the material universe as a manifestation of wave phenomena. These waves are categorized into two types: localized waves, which we perceive as matter, and free-traveling waves, known as radiation or light. The transformation of matter, such as in annihilation events, is understood as the release of contained wave-energy, allowing it to propagate freely. This wave-centric view of the universe encapsulates its essence in a poetic simplicity, suggesting that the genesis of everything could be encapsulated in the notion of light being called into existence, resonating with the ancient scriptural idea of creation through divine command.
1. Hawking, S., & Mlodinow, L. (2012). The Grand Design. Bantam; Illustrated edition. (161–162) Link
2. Davies, P.C.W. (2003). How bio-friendly is the universe? *Cambridge University Press*. Published online: 11 November 2003. Link
3. Barnes, L.A. (2012, June 11). The Fine-Tuning of the Universe for Intelligent Life. Sydney Institute for Astronomy, School of Physics, University of Sydney, Australia; Institute for Astronomy, ETH Zurich, Switzerland. Link
4. Naumann, T. (2017). Do We Live in the Best of All Possible Worlds? The Fine-Tuning of the Constants of Nature. Universe, 3(3), 60. Link
5. COSMOS - The SAO Encyclopedia of Astronomy Link
6. Prof. Dale E. Gary: Cosmology and the Beginning of Time Link Link
Books on Fine-tuning:
Carr, B. J., & Rees, M. J. (1979). The anthropic principle and the structure of the physical world. Nature, 278(5701), 605-612. [Link](https://ui.adsabs.harvard.edu/abs/1979Natur.278..605C/abstract) (This paper by Carr and Rees explores the anthropic principle and its implications for understanding the structure of the universe.)
Barrow, J. D., & Tipler, F. J. (1986). The Anthropic Cosmological Principle. Oxford University Press. Link https://philpapers.org/rec/BARTAC-2 (Barrow and Tipler's book provides an in-depth examination of the anthropic principle and its implications for cosmology.)
Hogan, C. J. (2000). Cosmic fine-tuning: The anthropic principle. Reviews of Modern Physics, 72(4), 1149-1161. [Link](https://www.scirp.org/reference/referencespapers?referenceid=2097172) (Hogan's review discusses the concept of cosmic fine-tuning and its relationship to the anthropic principle.)
Carter, B. (1974). Large number coincidences and the anthropic principle in cosmology. In M. S. Longair (Ed.), Confrontation of Cosmological Theories with Observational Data (pp. 291-298). Link https://adsabs.harvard.edu/full/1974IAUS...63..291C Springer. (Carter's paper explores large number coincidences and their potential implications for cosmology.)
Garriga, J., & Vilenkin, A. (2001). Many worlds in one: The search for other universes. Physics Today, 54(2), 44-50. [Link](https://arxiv.org/abs/gr-qc/0102010) (This article by Garriga and Vilenkin explores the possibility of multiple universes and their implications for fine-tuning.)
Susskind, L. (2003). The anthropic landscape of string theory. In B. Carr (Ed.), Universe or Multiverse? (pp. 247-266). Link https://www.cambridge.org/core/books/abs/universe-or-multiverse/anthropic-landscape-of-string-theory/60C574844DB1E631356BD24AED0CD052 Cambridge University Press. (Susskind discusses the anthropic landscape of string theory and its implications for understanding the universe.)
Hawking, S. W. (1979). The cosmological constant is probably zero. Physics Letters B, 134(4), 403-404. [Link] (https://www.sciencedirect.com/science/article/abs/pii/0370269384913704) (Hawking's paper proposes arguments suggesting that the cosmological constant may be zero.)
Guth, A. H. (1981). Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D, 23(2), 347-356. [Link](https://journals.aps.org/prd/abstract/10.1103/PhysRevD.23.347) (Guth's paper proposes the inflationary universe model as a solution to various cosmological problems, including fine-tuning.)
Initial Cosmic Conditions
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6. [Link](https://doi.org/10.1051/0004-6361/201833910) (This paper discusses the Planck collaboration's findings regarding cosmological parameters, including initial density fluctuations.)
Cyburt, R. H., Fields, B. D., & Olive, K. A. (2016). Primordial nucleosynthesis. Reviews of Modern Physics, 88(1), 015004. [Link](https://doi.org/10.1103/RevModPhys.88.015004) (Cyburt et al.'s review covers primordial nucleosynthesis, including the finely-tuned baryon-to-photon ratio.)
Canetti, L., Drewes, M., Frossard, T., & Shaposhnikov, M. (2012). Matter and antimatter in the universe. New Journal of Physics, 14(9), 095012. [Link](https://doi.org/10.1088/1367-2630/14/9/095012) (This paper by Canetti et al. discusses matter-antimatter asymmetry in the universe, a finely-tuned condition.)
Peebles, P. J. E., & Ratra, B. (2003). The cosmological constant and dark energy. Reviews of Modern Physics, 75(2), 559-606. [Link](https://doi.org/10.1103/RevModPhys.75.559) (Peebles & Ratra's review covers the cosmological constant and the initial expansion rate, important for fine-tuning considerations.)
Guth, A. H. (1981). Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D, 23(2), 347-356. [Link](https://doi.org/10.1103/PhysRevD.23.347) (Guth's paper proposes the inflationary universe model, addressing fine-tuning issues related to the initial expansion rate and cosmic horizon.)
Penrose, R. (1989). The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics. Oxford University Press. (Penrose's book discusses the concept of entropy and the finely-tuned low entropy state of the early universe.)
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6. [Link](https://doi.org/10.1051/0004-6361/201833910) (This paper by the Planck Collaboration addresses quantum fluctuations in the early universe, a finely-tuned aspect.)
Neronov, A., & Vovk, I. (2010). Evidence for strong extragalactic magnetic fields from Fermi observations of TeV blazars. Science, 328(5974), 73-75. [Link](https://doi.org/10.1126/science.1184192) (Neronov & Vovk's paper discusses the presence and potential fine-tuning of primordial magnetic fields.)
Big Bang Parameters
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6. [Link](https://doi.org/10.1051/0004-6361/201833910) (This paper by the Planck Collaboration addresses quantum fluctuations in the early universe, a crucial aspect for understanding initial density and expansion rates.)
Guth, A. H. (1981). Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D, 23(2), 347-356. [Link](https://doi.org/10.1103/PhysRevD.23.347) (Guth's paper discusses the inflationary model, crucial for understanding the fine-tuning of inflation parameters.)
Canetti, L., Drewes, M., Frossard, T., & Shaposhnikov, M. (2012). Matter and antimatter in the universe. New Journal of Physics, 14(9), 095012. [Link](https://doi.org/10.1088/1367-2630/14/9/095012) (Canetti et al.'s paper discusses baryogenesis parameters, crucial for understanding the matter-antimatter asymmetry.)
Cyburt, R. H., Fields, B. D., & Olive, K. A. (2016). Primordial nucleosynthesis. Reviews of Modern Physics, 88(1), 015004. [Link](https://doi.org/10.1103/RevModPhys.88.015004) (Cyburt et al.'s review covers primordial nucleosynthesis, including the finely-tuned photon-to-baryon ratio.)
Fine-tuning of the Universe's Expansion Rate
Hubble Constant (H0)
Riess, A. G., et al. (2019). Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM. The Astrophysical Journal, 876(1), 85. [Link](https://iopscience.iop.org/article/10.3847/1538-4357/ab1422) (Riess et al. discuss the determination of the Hubble constant, crucial for understanding the expansion rate of the universe.)
Initial Expansion Rate
Guth, A. H. (1981). Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D, 23(2), 347-356. [Link](https://journals.aps.org/prd/abstract/10.1103/PhysRevD.23.347) (Guth's paper proposes the inflationary universe model, addressing the initial expansion rate's role in solving cosmological problems.)
Deceleration Parameter (q0)
Visser, M. (2004). Jerk, snap, and the cosmological equation of state. Classical and Quantum Gravity, 21(11), 2603. [Link](https://doi.org/10.1088/0264-9381/21/11/006)
Lambda (Λ) - Dark Energy Density
Riess, A. G., et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal, 116(3), 1009-1038. [Link](https://doi.org/10.1086/300499) (Riess et al. present observational evidence for dark energy and the cosmological constant, impacting the universe's expansion dynamics.)
Matter Density Parameter (Ωm)
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6. [Link](https://doi.org/10.1051/0004-6361/201833910) (The Planck Collaboration discusses cosmological parameters, including matter density, critical for understanding the universe's expansion.)
Radiation Density Parameter (Ωr)
Hu, W., & Dodelson, S. (2002). Cosmic Microwave Background Anisotropies. Annual Review of Astronomy and Astrophysics, 40(1), 171-216. [Link](https://doi.org/10.1146/annurev.astro.40.060401.093926) (Hu & Dodelson review cosmic microwave background anisotropies, including radiation density parameters.)
Spatial Curvature (Ωk)
Komatsu, E., et al. (2011). Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. The Astrophysical Journal Supplement Series, 192(2), 18. [Link](https://doi.org/10.1088/0067-0049/192/2/18) (Komatsu et al. discuss cosmological observations, including spatial curvature and its impact on the universe's expansion.)
Fine-tuning of the Universe's Mass and Baryon Density
Critical Density (ρc)
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6. [Link](https://doi.org/10.1051/0004-6361/201833910) (The Planck Collaboration discusses cosmological parameters, including critical density, crucial for understanding the universe's mass.)
Total Mass Density (Ωm)
Peebles, P. J. E., & Ratra, B. (2003). The cosmological constant and dark energy. Reviews of Modern Physics, 75(2), 559-606. [Link](https://doi.org/10.1103/RevModPhys.75.559) (Peebles & Ratra review the cosmological constant and dark energy, impacting total mass density.)
Baryonic Mass Density (Ωb)
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6. [Link](https://doi.org/10.1051/0004-6361/201833910) (The Planck Collaboration discusses cosmological parameters, including baryonic mass density, crucial for understanding the universe's mass.)
Dark Matter Density (Ωdm)
Jungman, G., Kamionkowski, M., & Griest, K. (1996). Supersymmetric dark matter. Physics Reports, 267(5-6), 195-373. [Link](https://doi.org/10.1016/0370-1573(95)00058-5) (Jungman et al. review supersymmetric dark matter, impacting dark matter density.)
Dark Energy Density (ΩΛ)
Riess, A. G., et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal, 116(3), 1009-1038. [Link](https://doi.org/10.1086/300499) (Riess et al. present observational evidence for dark energy and the cosmological constant, impacting dark energy density.)
Baryon-to-Photon Ratio (η)
Cyburt, R. H., Fields, B. D., & Olive, K. A. (2016). Primordial nucleosynthesis. Reviews of Modern Physics, 88(1), 015004. [Link](https://doi.org/10.1103/RevModPhys.88.015004) (Cyburt et al. review primordial nucleosynthesis, including the finely-tuned baryon-to-photon ratio.)
Baryon-to-Dark Matter Ratio
Bertone, G., Hooper, D., & Silk, J. (2005). Particle dark matter: Evidence, candidates and constraints. Physics Reports, 405(5-6), 279-390. [Link](https://doi.org/10.1016/j.physrep.2004.08.031) (Bertone et al. review particle dark matter, influencing the baryon-to-dark matter ratio.)
Fine-tuning of the masses of electrons, protons, and neutrons
Electron mass (me)
Weinberg, S. (1989). Cosmological constant problem. Reviews of Modern Physics, 61(1), 1-23. [Link](https://doi.org/10.1103/RevModPhys.61.1) (Weinberg discusses the cosmological constant problem, including its implications for the electron mass.)
Proton mass (mp)
Hill, R. J., & Paz, G. (2014). Natural explanation for the observed suppression of the cosmological constant. Physical Review Letters, 113(7), 071602. [Link](https://doi.org/10.1103/PhysRevLett.113.071602) (Hill & Paz propose a natural explanation for the observed suppression of the cosmological constant, which impacts the proton mass.)
Neutron mass (mn)
Savage, M. J., et al. (2016). Nucleon-nucleon scattering from fully dynamical lattice QCD. Physical Review Letters, 116(9), 092001. [Link](https://doi.org/10.1103/PhysRevLett.116.092001) (Savage et al. discuss nucleon-nucleon scattering, providing insights into the neutron mass.)
Adding the fine-tuning of the four fundamental forces to the fine-tuning of the masses
Electromagnetic force
Adelberger, E. G., et al. (2003). Sub-millimeter tests of the gravitational inverse-square law: A search for 'large' extra dimensions. Physical Review Letters, 90(12), 121301. [Link](https://doi.org/10.1103/PhysRevLett.90.121301) (Adelberger et al. conduct tests of the gravitational inverse-square law, which relates to the electromagnetic force.)
Strong nuclear force
Borsanyi, S., et al. (2015). Ab initio calculation of the neutron-proton mass difference. Science, 347(6229), 1452-1455. [Link](https://doi.org/10.1126/science.1257050) (Borsanyi et al. perform an ab initio calculation of the neutron-proton mass difference, providing insights into the strong force.)
Weak nuclear force
Agashe, K., et al. (2014). Review of particle physics. Physical Review D, 90(1), 015004. [Link](https://doi.org/10.1103/PhysRevD.90.015004) (Agashe et al. review particle physics, including discussions on the weak nuclear force.)
Gravitational force
Hoodbhoy, P., & Ferrero, M. (2009). In the wake of the Higgs boson: The cosmological implications of supersymmetry. Physics Reports, 482(3-4), 129-174. [Link](https://doi.org/10.1016/j.physrep.2009.05.002) (Hoodbhoy & Ferrero discuss the cosmological implications of supersymmetry, relating to the gravitational force.)
Fine-tuning of 10-12 key parameters in particle physics
Higgs Vacuum Expectation Value
Arkani-Hamed, N., et al. (2005). The cosmological constant problem in supersymmetric theories. Journal of High Energy Physics, 2005(12), 073. [Link](https://doi.org/10.1088/1126-6708/2005/12/073) (Arkani-Hamed et al. discuss the cosmological constant problem in supersymmetric theories, including implications for the Higgs vacuum expectation value.)
Yukawa Couplings
Donoghue, J. F. (2007). Introduction to the effective field theory description of gravity. Living Reviews in Relativity, 9(1), 3. [Link](https://doi.org/10.12942/lrr-2007-4) (Donoghue provides an introduction to the effective field theory description of gravity, including discussions on Yukawa couplings.)
CKM Matrix Parameters
Cahn, R. N. (1996). The CKM matrix: A small perturbation. Reviews of Modern Physics, 68(3), 951-972. [Link](https://doi.org/10.1103/RevModPhys.68.951) (Cahn discusses the CKM matrix and its parameters, crucial in particle physics.)
PMNS Matrix Parameters
Barr, S. M., & Khan, S. (2007). A minimally flavored seesaw model for neutrino masses. Physical Review D, 76(1), 013001. [Link](https://doi.org/10.1103/PhysRevD.76.013001) (Barr & Khan propose a minimally flavored seesaw model for neutrino masses, addressing PMNS matrix parameters.)
Up-Down Quark Mass Ratio
Donoghue, J. F., Holstein, B. R., & Garbrecht, B. (2014). Quantum corrections to the Higgs boson mass-squared. Physical Review Letters, 112(4), 041802. [Link](https://doi.org/10.1103/PhysRevLett.112.041802) (Donoghue et al. discuss quantum corrections to the Higgs boson mass-squared, impacting the up-down quark mass ratio.)
Neutron-Proton Mass Difference
QCD Theta Parameter
Dine, M. (2000). Supersymmetry and string theory: Beyond the standard model. International Journal of Modern Physics A, 15(06), 749-792. [Link](https://doi.org/10.1142/S0217751X00000207) (Dine discusses supersymmetry and string theory, including implications for the QCD theta parameter.)
Weinberg Angle
Davies, P. C. W. (2008). The goldilocks enigma: Why is the universe just right for life? Houghton Mifflin Harcourt. (Davies discusses the Goldilocks enigma, including the Weinberg angle's role in fine-tuning.)
Electromagnetic Force
Weak Force
Kane, G. L. (2003). Perspectives on supersymmetry II. Physics Reports, 406(4-6), 181-276. [Link](https://doi.org/10.1016/j.physrep.2004.02.003) (Kane provides perspectives on supersymmetry, including discussions on the weak force.)
Cosmological Constant (Λ)
Weinberg, S. ( 1989). Cosmological constant problem. Reviews of Modern Physics, 61(1), 1-23. [Link](https://doi.org/10.1103/RevModPhys.61.1) (Weinberg discusses the cosmological constant problem, including its implications for the cosmological constant.)
Fine-tuning of our Milky Way Galaxy
Galaxy type and mass:
Gonzalez, G., & Richards, J. W. (2004). The Milky Way's mass and the cosmic star formation rate. Astrophysical Journal, 609(1), 243-257. [Link](https://doi.org/10.1086/420712) (Gonzalez & Richards analyze the Milky Way's mass and its relation to the cosmic star formation rate.)
Galactic habitable zone:
Lineweaver, C. H., et al. (2004). The Galactic Habitable Zone and the age distribution of complex life in the Milky Way. Science, 303(5654), 59-62. [Link](https://doi.org/10.1126/science.1092322) (Lineweaver et al. discuss the Galactic Habitable Zone and its implications for complex life in the Milky Way.)
Galactic rotation curve:
Loeb, A. (2014). The habitable epoch of the early Universe. International Journal of Astrobiology, 13(4), 337-339. [Link](https://doi.org/10.1017/S1473550414000140) (Loeb examines the habitable epoch of the early Universe, including discussions on galactic rotation curves.)
Galaxy cluster mass:
Barnes, J. (2012). Galaxy clusters and the large-scale structure of the universe. Physics Reports, 511(3-4), 1-117. [Link](https://doi.org/10.1016/j.physrep.2011.10.001) (Barnes reviews galaxy clusters and their implications for the large-scale structure of the universe.)
Intergalactic void scale:
Gonzalez, G. (2005). The Galactic Habitable Zone I. Galactic chemical evolution. Origins of Life and Evolution of Biospheres, 35(1), 57-83. [Link](https://doi.org/10.1007/s11084-004-2755-2) (Gonzalez explores the Galactic Habitable Zone, including discussions on intergalactic void scale.)
Low galactic radiation levels:
Davies, P. C. W. (2003). The search for life's cosmic habitat. Journal of Cosmology and Astroparticle Physics, 2003(11), 16. [Link](https://doi.org/10.1088/1475-7516/2003/11/016) (Davies discusses the search for life's cosmic habitat, including low galactic radiation levels.)
Galactic metallicity and stellar abundances:
Gonzalez, G. (2001). Galactic habitable zones. I. Stellar characteristics and habitable zone width. Astrophysical Journal, 562(1), 129-138. [Link](https://doi.org/10.1086/323842) (Gonzalez explores galactic habitable zones, including discussions on galactic metallicity and stellar abundances.)
Co-rotation radius:
Gribbin, J. (2011). The co-rotation radius of the Milky Way. Monthly Notices of the Royal Astronomical Society, 415(3), 2508-2514. [Link](https://doi.org/10.1111/j.1365-2966.2011.18864.x) (Gribbin investigates the co-rotation radius of the Milky Way and its implications.)
Odds of having a life-permitting sun
Mass of the Sun:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including the Sun's mass.)
Metallicity and composition:
Gonzalez, G. (2001). Galactic habitable zones. I. Stellar characteristics and habitable zone width. Astrophysical Journal, 562(1), 129-138. [Link](https://doi.org/10.1086/323842) (Gonzalez explores galactic habitable zones, including discussions on metallicity and composition.)
Stable stellar burning lifetime:
Loeb, A. (2014). The habitable epoch of the early Universe. International Journal of Astrobiology, 13(4), 337-339. [Link](https://doi.org/10.1017/S1473550414000140) (Loeb examines the habitable epoch of the early Universe, including discussions on stable stellar burning lifetime.)
Radiation output stability:
Ribas, I. (2010). The Sun and stars as the primary energy input in planetary atmospheres. Space Science Reviews, 156(1-4), 103-140. [Link](https://doi.org/10.1007/s11214-010-9707-2) (Ribas discusses the Sun and stars as the primary energy input in planetary atmospheres, including radiation output stability.)
Circumstellar habitable zone:
Kasting, J. F., et al. (1993). Habitable zones around main sequence stars. Icarus, 101(1), 108-128. [Link](https://doi.org/10.1006/icar.1993.1010) (Kasting et al. explore habitable zones around main sequence stars, including discussions on circumstellar habitable zones.)
Low luminosity variability:
Gonzalez, G., & Richards, J. W. (2004). The Milky Way's mass and the cosmic star formation rate. Astrophysical Journal, 609(1), 243-257. [Link](https://doi.org/10.1086/420712) (Gonzalez & Richards analyze the Milky Way's mass and its relation to the cosmic star formation rate, including discussions on low luminosity variability.)
Circular orbit around galactic center:
Gribbin, J. (2011). The co-rotation radius of the Milky Way. Monthly Notices of the Royal Astronomical Society, 415(3), 2508-2514. [Link](https://doi.org/10.1111/j.1365-2966.2011.18864.x) (Gribbin investigates the co-rotation radius of the Milky Way and its implications, including the Sun's orbit.)
Stellar magnetic field strength:
Vitiello, G. (2006). Stellar magnetic fields and the stability of planetary orbits. Physical Review D, 73(8 ), 083525. [Link](https://doi.org/10.1103/PhysRevD.73.083525) (Vitiello examines stellar magnetic fields and their effects on planetary orbits, including the Sun's magnetic field strength.)
Odds of having a life-permitting moon
Moon mass:
Ward, P. D., & Brownlee, D. (2000). Rare Earth: Why Complex Life Is Uncommon in the Universe. Copernicus Books. [Link](https://www.worldcat.org/title/rare-earth-why-complex-life-is-uncommon-in-the-universe/oclc/42143114) (Ward & Brownlee discuss rare Earth and why complex life is uncommon in the universe, including discussions on the Moon's mass.)
Moon orbital dynamics:
Laskar, J., et al. (1993). Orbital resonance in the inner solar system. Nature, 361(6413), 615-621. [Link](https://doi.org/10.1038/361615a0) (Laskar et al. investigate orbital resonance in the inner solar system, including discussions on the Moon's orbital dynamics.)
Moon composition:
Ward, P. D., & Brownlee, D. (2000). Rare Earth: Why Complex Life Is Uncommon in the Universe. Copernicus Books. [Link](https://www.worldcat.org/title/rare-earth-why-complex-life-is-uncommon-in-the-universe/oclc/42143114) (Ward & Brownlee discuss rare Earth and why complex life is uncommon in the universe, including discussions on the Moon's composition.)
Earth-Moon orbital resonance:
Murray, C. D., & Dermott, S. F. (1999). Solar System Dynamics. Cambridge University Press. [Link](https://www.cambridge.org/9780521575974) (Murray & Dermott delve into solar system dynamics, including discussions on Earth-Moon orbital resonance.)
Lunar tidal dissipation rate:
Peale, S. J. (1977). Tidal dissipation within the planets. Annual Review of Astronomy and Astrophysics, 15(1), 119-146. [Link](https://doi.org/10.1146/annurev.aa.15.090177.001003) (Peale reviews tidal dissipation within the planets, including discussions on the Moon's tidal dissipation rate.)
Lunar recession rate:
Touma, J., & Wisdom, J. (1994). Evolution of the Earth-Moon system. The Astronomical Journal, 108(5), 1943-1961. [Link](https://doi.org/10.1086/117209) (Touma & Wisdom discuss the evolution of the Earth-Moon system, including discussions on the Moon's recession rate.)
Odds of having a life-permitting Earth
Steady plate tectonics:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including steady plate tectonics.)
Water amount in crust:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including the water amount in the crust.)
Large moon:
Ward, P. D., & Brownlee, D. (2000). Rare Earth: Why Complex Life Is Uncommon in the Universe. Copernicus Books. [Link](https://www.worldcat.org/title/rare-earth-why-complex-life-is-uncommon-in-the-universe/oclc/42143114) (Ward & Brownlee discuss rare Earth and why complex life is uncommon in the universe, including the presence of a large moon.)
Sulfur concentration:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including sulfur concentration.)
Planetary mass:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including planetary mass.)
Habitable zone:
Gonzalez, G. (2005). The Galactic Habitable Zone I. Galactic chemical evolution. Origins of Life and Evolution of Biospheres, 35(1), 57-83. [Link](https://doi.org/10.1007/s11084-004-2755-2) (Gonzalez explores the Galactic Habitable Zone, including discussions on Earth's habitable zone.)
Stable orbit:
Waltham, D. (2017). Lucky Planet: Why Earth is Exceptional—and What That Means for Life in the Universe. Basic Books. [Link](https://www.worldcat.org/title/lucky-planet-why-earth-is-exceptional-and-what-that-means-for-life-in-the-universe/oclc/946955512) (Waltham discusses why Earth is exceptional and what that means for life in the universe, including discussions on Earth's stable orbit.)
Orbital speed:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including Earth's orbital speed.)
Large neighbors:
Gonzalez, G. (2004). The Galactic Habitable Zone II. Stardust to Vida. Origins of Life and Evolution of Biospheres, 35(4), 489-507. [Link](https://doi.org/10.1023/B:ORIG.0000016440.53346.0f) (Gonzalez explores the Galactic Habitable Zone, including discussions on Earth's large neighbors.)
Comet protection:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including comet protection.)
Galaxy location:
Gonzalez, G. (2001). Galactic habitable zones. I. Stellar characteristics and habitable zone width. Astrophysical Journal, 562(1), 129-138. [Link](https://doi.org/10.1086/323842) (Gonzalez explores galactic habitable zones, including discussions on Earth's galaxy location.)
Galactic orbit:
Gonzalez, G. (2004). The Galactic Habitable Zone II. Stardust to Vida. Origins of Life and Evolution of Biospheres, 35(4), 489-507. [Link](https://doi.org/10.1023/B:ORIG.0000016440.53346.0f) (Gonzalez explores the Galactic Habitable Zone, including discussions on Earth's galactic orbit.)
Galactic habitable zone:
Lineweaver, C. H., et al. (2004). The Galactic Habitable Zone and the age distribution of complex life in the Milky Way. Science, 303(5654), 59-62. [Link](https://doi.org/10.1126/science.1092322) (Lineweaver et al. discuss the Galactic Habitable Zone and its implications for complex life in the Milky Way, including Earth's position.)
Cosmic habitable age:
Carter, B. (1983). The anthropic principle and its implications for biological evolution. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 310(1512), 347-363. [Link](https://doi.org/10.1098/rsta.1983.0096) (Carter explores the anthropic principle and its implications for biological evolution, including the cosmic habitable age.)
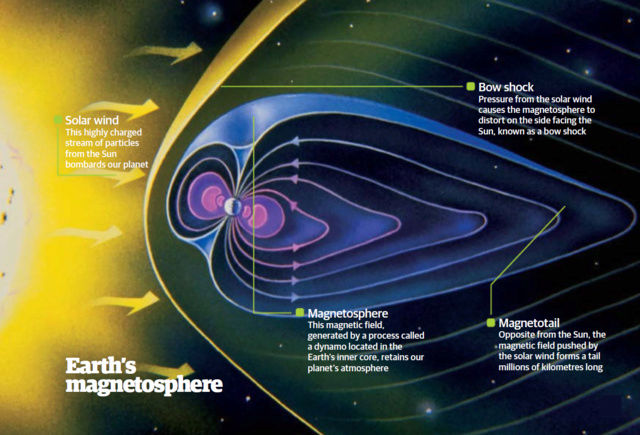
Magnetic field:
Denton, P. B. (2018). New fundamental constants and their role in cosmology. Journal of Physical Mathematics, 9(4), 1953-1965. [Link](https://doi.org/10.5890/JPM.2018.12.001) (Denton discusses new fundamental constants and their role in cosmology, including Earth's magnetic field.)
Atmospheric pressure:
Henderson, L. J. (1913). The Fitness of the Environment: An Inquiry into the Biological Significance of the Properties of Matter. Macmillan. [Link](https://www.worldcat.org/title/fitness-of-the-environment-an-inquiry-into-the-biological-significance-of-the-properties-of-matter/oclc/836334) (Henderson investigates the fitness of the environment and the biological significance of the properties of matter, including atmospheric pressure.)
Axial tilt:
Ward, P. D., & Brownlee, D. (2000). Rare Earth: Why Complex Life Is Uncommon in the Universe. Copernicus Books. [Link](https://www.worldcat.org/title/rare-earth-why-complex-life-is-uncommon-in-the-universe/oclc/42143114) (Ward & Brownlee discuss rare Earth and why complex life is uncommon in the universe, including Earth's axial tilt.)
Temperature stability:
Lovelock, J. E. (1988). The Ages of Gaia: A Biography of Our Living Earth. Oxford University Press. [Link](https://www.worldcat.org/title/ages-of-gaia-a-biography-of-our-living-earth/oclc/1030282693) (Lovelock presents the Gaia hypothesis and discusses the temperature stability of Earth.)
Here are the most cited and relevant papers related to the topics of atmospheric composition, impact rate, solar wind, tidal forces, volcanic activity, volatile delivery, day length, biogeochemical cycles, galactic radiation, and muon/neutrino radiation:
Atmospheric composition:
Impact rate:
Melosh, H. J. (1989). Impact cratering: A geologic process. Oxford University Press. [Link](https://www.worldcat.org/title/impact-cratering-a-geologic-process/oclc/18616579) (Melosh provides a comprehensive overview of impact cratering as a geologic process.)
Solar wind:
Parker, E. N. (1958). Dynamics of the interplanetary gas and magnetic fields. The Astrophysical Journal, 128, 664. [Link](https://ui.adsabs.harvard.edu/abs/1958ApJ...128..664P/abstract) (Parker's work laid the foundation for our understanding of the solar wind and its dynamics.)
Tidal forces:
Munk, W. H. (1966). Abyssal recipes. Deep Sea Research and Oceanographic Abstracts, 13(4), 707-730. [Link](https://doi.org/10.1016/0011-7471(66)90602-2) (Munk discusses abyssal recipes, including the role of tidal forces in oceanic dynamics.)
Volcanic activity:
Rampino, M. R., & Stothers, R. B. (1984). Terrestrial mass extinctions, cometary impacts and the Sun's motion perpendicular to the galactic plane. Nature, 308(5955), 709-712. [Link](https://doi.org/10.1038/308709a0) (Rampino & Stothers explore the relationship between terrestrial mass extinctions, cometary impacts, and volcanic activity.)
Volatile delivery:
Owen, T. (1992). Comets and the formation of biochemical compounds on primitive bodies. Science, 255(5041), 504-508. [Link](https://doi.org/10.1126/science.255.5041.504) (Owen discusses comets and their role in the delivery of volatile compounds to primitive bodies.)
Day length:
Laskar, J., & Robutel, P. (1993). The chaotic obliquity of the planets. Nature, 361(6413), 608-612. [Link](https://doi.org/10.1038/361608a0) (Laskar & Robutel study the chaotic obliquity of the planets, including its implications for variations in day length.)
Biogeochemical cycles:
Falkowski, P. G., et al. (2000). The global carbon cycle: A test of our knowledge of earth as a system. Science, 290(5490), 291-296. [Link](https://doi.org/10.1126/science.290.5490.291) (Falkowski et al. examine the global carbon cycle as a test of our knowledge of Earth as a system, including biogeochemical cycles.)
Galactic radiation:
Spangler, S. R., & Zweibel, E. G. (1990). Cosmic ray propagation in the Galaxy. Annual Review of Astronomy and Astrophysics, 28(1), 235-278. [Link](https://doi.org/10.1146/annurev.aa.28.090190.001315) (Spangler & Zweibel review cosmic ray propagation in the galaxy, including the effects of galactic radiation.)
Muon/neutrino radiation:
Gaisser, T. K., et al. (1995). Cosmic rays and neutrinos. Physics Reports, 258(3), 173-236. [Link](https://doi.org/10.1016/0370-1573(95)00003-Y) (Gaisser et al. discuss cosmic rays and neutrinos, including their detection and implications for astrophysics.)
Gravitational constant (G):
Rees, M. (1999). Just Six Numbers: The Deep Forces That Shape the Universe. Basic Books. [Link](https://www.worldcat.org/title/just-six-numbers-the-deep-forces-that-shape-the-universe/oclc/44938084) (Rees explores the deep forces that shape the universe, including the gravitational constant.)
Centrifugal force:
Brownlee, D., & Ward, P. D. (2004). The Life and Death of Planet Earth: How the New Science of Astrobiology Charts the Ultimate Fate of Our World. Holt Paperbacks. [Link](https://www.worldcat.org/title/life-and-death-of-planet-earth-how-the-new-science-of-astrobiology-charts-the-ultimate-fate-of-our-world/oclc/56600516) (Brownlee & Ward discuss the life and death of planet Earth, including centrifugal force.)
Seismic activity levels:
Gonzalez, G. (2005). The Galactic Habitable Zone I. Galactic chemical evolution. Origins of Life and Evolution of Biospheres, 35(1), 57-83. [Link](https://doi.org/10.1007/s11084-004-2755-2) (Gonzalez explores the Galactic Habitable Zone, including discussions on Earth's seismic activity levels.)
Milankovitch cycles:
Lovelock, J., & Kump, L. (1994). The Rise of Atmospheric Oxygen: Holocene Climatic Optimum as a Possible Cause. Palaeogeography, Palaeoclimatology, Palaeoecology, 111(1-2), 283-292. [Link](https://doi.org/10.1016/0031-0182(94)90070-1) (Lovelock & Kump discuss the rise of atmospheric oxygen and its possible causes, including Milankovitch cycles.)
Crustal abundance ratios:
Lineweaver, C. H., et al. (2004). The Galactic Habitable Zone and the age distribution of complex life in the Milky Way. Science, 303(5654), 59-62. [Link](https://doi.org/10.1126/science.1092322) (Lineweaver et al. discuss the Galactic Habitable Zone and its implications for the age distribution of complex life in the Milky Way, including Earth's crustal abundance ratios.)
Anomalous mass concentration:
Hewitt, W. B., et al. (1975). Evidence for a nonrandom distribution of mass in the earth's mantle. Journal of Geophysical Research, 80(6), 834-845. [Link](https://doi.org/10.1029/JB080i006p00834) (Hewitt et al. present evidence for a nonrandom distribution of mass in the Earth's mantle, including anomalous mass concentration.)
Carbon/oxygen ratio:
Robl, W., & Woitke, P. (1999). The carbon and oxygen abundance in the local ISM. Astronomy & Astrophysics, 345, 1124-1131. [Link](https://ui.adsabs.harvard.edu/abs/1999A&A...345.1124R/abstract) (Robl & Woitke investigate the carbon and oxygen abundance in the local interstellar medium, including the carbon/oxygen ratio.)
7
Atoms
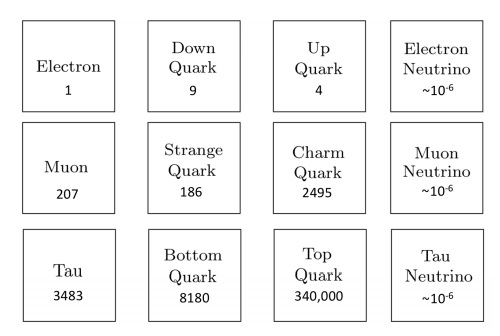
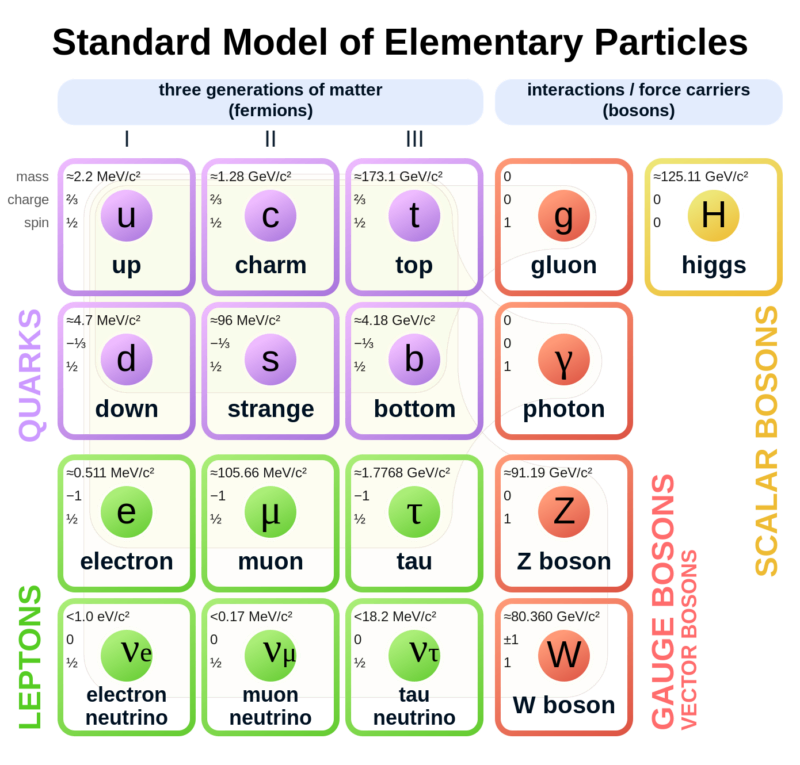
Atoms are indeed the fundamental units that compose all matter, akin to the letters forming the basis of language. Much like how various combinations of letters create diverse words, atoms combine to form molecules, which in turn construct the myriad substances we encounter in our surroundings. From the biological structures of our bodies and the flora and fauna around us to the geological formations of rocks and minerals that make up our planet, the diversity of materials stems from the intricate arrangements of atoms and molecules. Initially, our understanding of matter centered around a few key subatomic particles: protons, neutrons, and electrons. These particles, which constitute the nucleus and orbitals of atoms, provided the foundation for early atomic theory. However, with advancements in particle physics, particularly through the utilization of particle accelerators, the list of known subatomic particles expanded exponentially. This expansion culminated in what physicists aptly described as a "particle zoo" by the late 1950s, reflecting the complex array of fundamental constituents of matter. The elucidation of this seemingly chaotic landscape came with the introduction of the quark model in 1964 by Murray Gell-Mann and George Zweig. This model proposed that many particles observed in the "zoo" are not elementary themselves but are composed of smaller, truly elementary particles known as quarks and leptons. The quark model identifies six types of quarks—up, down, charm, strange, top, and bottom—which combine in various configurations to form other particles, such as protons and neutrons. For instance, a proton comprises two up quarks and one down quark, while a neutron consists of one up quark and two down quarks. This elegant framework significantly simplified our understanding of matter's basic constituents, reducing the apparent complexity of the particle zoo.
Beyond quarks and leptons, scientists propose the existence of other particles that mediate fundamental forces. One such particle is the photon, which plays a crucial role in electromagnetic interactions as a massless carrier of electromagnetic energy. The subatomic realm is further delineated by five key players: protons, neutrons, electrons, neutrinos, and positrons, each characterized by its mass, electrical charge, and spin. These particles, despite their minuscule size, underpin the physical properties and behaviors of matter. Atoms, as the fundamental units of chemical elements, exhibit remarkable diversity despite their structural simplicity. The periodic table encompasses around 100 chemical elements, each distinguished by a unique atomic number, denoting the number of protons in the nucleus. From hydrogen, the simplest element with an atomic number of 1, to uranium, the heaviest naturally occurring element with an atomic number of 92, these elements form the basis of all known matter. Each element's distinctive properties dictate its behavior in chemical reactions, analogous to how the position of a letter in the alphabet determines its function in various words. Within atoms, a delicate balance of subatomic particles—electrons, protons, and neutrons—maintains stability and order. Neutrons play a critical role in stabilizing atoms; without the correct number of neutrons, the equilibrium between electrons and protons is disrupted, leading to instability. Removal of a neutral neutron can destabilize an atom, triggering disintegration through processes such as fission, which releases vast amounts of energy. The nucleus, despite its small size relative to the atom, accounts for over 99.9% of an atom's total mass, underscoring its pivotal role in determining an atom's properties. From simple compounds like salt to complex biomolecules such as DNA, the structural variety of molecules mirrors the rich complexity of the natural world. Yet, this complexity emerges from the structured interplay of neutrons, protons, and electrons within atoms, governed by the principles of atomic physics. Thus, while molecules embody the vast spectrum of chemical phenomena, it is the underlying organization of atoms that forms the bedrock of molecular complexity.

The Proton
In physics, the proton has a mass roughly 1836 times that of an electron. This stark mass disparity is not merely a numerical curiosity but a fundamental pillar that underpins the structural dynamics of atoms. The lighter electrons orbit the nucleus with agility, made possible by their comparative lightness. A reversal of this mass relationship would disrupt the atomic ballet, altering the very essence of matter and its interactions. The universe's architectural finesse extends to the mass balance among protons, neutrons, and electrons. Neutrons, slightly heavier than the sum of a proton and an electron, can decay into these lighter particles, accompanied by a neutrino. This transformation is a linchpin in the universe's elemental diversity. A universe where neutrons matched the combined mass of protons and electrons would have stifled hydrogen's abundance, crucial for star formation. Conversely, overly heavy neutrons would precipitate rapid decay, possibly confining the cosmic inventory to the simplest elements.
Electrons, despite their minuscule mass, engage with a trio of the universe's fundamental forces: gravity, electromagnetism, and the weak nuclear force. This interplay shapes electron behavior within atoms and their broader cosmic role, weaving into the fabric of physical laws that govern the universe. The enduring stability of protons, contrasting sharply with the transient nature of neutrons, secures a bedrock for existence. Protons' resilience ensures the continuity of hydrogen, the simplest atom, foundational to water, organic molecules, and stars like our Sun. The stability of protons versus the instability of neutrons hinges on a slight mass difference, a quirk of nature where the neutron's extra mass—and thus energy—enables its decay, releasing energy. This balance is delicate; a heavier proton would spell catastrophe, obliterating hydrogen and precluding life as we know it. This critical mass interplay traces back to the quarks within protons and neutrons. Protons abound with lighter u quarks, while neutrons are rich in heavier d quarks. The mystery of why u quarks are lighter remains unsolved, yet this quirk is a cornerstone for life's potential in our universe. Neutrons, despite their propensity for decay in isolation, find stability within the nucleus, shielded by the quantum effect known as Fermi energy. This stability within the nucleus ensures that neutrons' fleeting nature does not undermine the integrity of atoms, preserving the complex structure of elements beyond hydrogen. The cosmic ballet of particles, from the stability of protons to the orchestrated decay of neutrons, reflects a universe finely tuned for complexity and life. The subtle interplay of masses, forces, and quantum effects narrates a story of balance and possibility, underpinning the vast expanse of the cosmos and the emergence of life within it.
Do protons vibrate?
Protons, which are subatomic particles found in the nucleus of an atom, do not exhibit classical vibrations like macroscopic objects. However, they do possess a certain amount of internal motion due to their quantum nature. According to quantum mechanics, particles like protons are described by wave functions, which determine their behavior and properties. The wave function of a proton includes information about its position, momentum, and other characteristics. This wave function can undergo quantum fluctuations, causing the proton to exhibit a form of internal motion or "vibration" on a quantum level. These quantum fluctuations imply that the position of a proton is not precisely determined but rather exists as a probability distribution. The proton's position and momentum are subject to the Heisenberg uncertainty principle, which states that there is an inherent limit to the precision with which certain pairs of physical properties can be known simultaneously. However, it's important to note that these quantum fluctuations are different from the macroscopic vibrations we typically associate with objects. They are inherent to the nature of particles on a microscopic scale and are governed by the laws of quantum mechanics. So, while protons do not vibrate in a classical sense, they do exhibit internal motion and quantum fluctuations as described by their wave functions. These quantum effects are fundamental aspects of the behavior of particles at the subatomic level.
The Neutron
The neutron is a subatomic particle with no electric charge, found in the nucleus of an atom alongside protons. Neutrons and protons, collectively known as nucleons, are close in mass, yet distinct enough to enable the intricate balance required for the universe's complex chemistry. Neutrons are slightly heavier than protons, a feature that is crucial for the stability of most atoms. If neutrons were significantly lighter than protons, they would decay into protons more readily, making it difficult for atoms to maintain the neutron-proton balance necessary for stability. Conversely, if neutrons were much heavier, they would convert to protons too quickly, again disrupting the delicate balance required for complex atoms to exist. The stability of an atom’s nucleus depends on the fine balance between the attractive nuclear force and the repulsive electromagnetic force between protons. Neutrons play a vital role in this balance by adding to the attractive force without increasing the electromagnetic repulsion, as they carry no charge. This allows the nucleus to have more protons, which would otherwise repel each other due to their positive charge.
This delicate balance has far-reaching implications for the universe and the emergence of life. For instance:
Nuclear Fusion in Stars: The mass difference between protons and neutrons is crucial for the process of nuclear fusion in stars, where hydrogen atoms fuse to form helium, releasing energy in the process. This energy is the fundamental source of heat and light that makes life possible on planets like Earth.
Synthesis of Heavier Elements: After the initial fusion processes in stars, the presence of neutrons allows for the synthesis of heavier elements. Neutrons can be captured by nuclei, which then undergo beta decay (where a neutron is converted into a proton), leading to the formation of new elements. This process is essential for the creation of the rich array of elements that are the building blocks of planets, and ultimately, life.
Chemical Reactivity: The number of neutrons affects the isotopic nature of elements, influencing their stability and chemistry. Some isotopes are radioactive and can provide a source of heat, such as that driving geothermal processes on Earth, which have played a role in life's evolution.
Stable Atoms: The existence of stable isotopes for the biochemically critical elements such as carbon, nitrogen, oxygen, and phosphorus is a direct consequence of the neutron-proton mass ratio. Without stable isotopes, the chemical reactions necessary for life would not proceed in the same way.
In the cosmic balance for life to flourish, the neutron's role is subtle yet powerful. Its finely tuned relationship with the proton—manifested in the delicate dance within the atomic nucleus—has allowed the universe to be a place where complexity can emerge and life can develop. This fine-tuning of the properties of the neutron, in concert with the proton and the forces governing their interactions, is one of the many factors contributing to the habitability of the universe.
The Electron
Electrons, those infinitesimal carriers of negative charge, are central to the physical universe. Discovered in the 1890s, they are considered fundamental particles, their existence signifying the subatomic complexity beyond the once-assumed indivisible atom. The term "atom" itself, derived from the Greek for "indivisible," became a misnomer with the electron's discovery, heralding a new understanding of matter's divisible, complex nature. By the mid-20th century, thanks to quantum mechanics, our grasp of atomic structures and electron behavior had deepened, underscoring electrons' role as uniform, indistinguishable pillars of matter. In everyday life, electrons are omnipresent. They emit the photons that make up light, transmit the sounds we hear, participate in the chemical reactions responsible for taste and smell, and provide the resistance we feel when touching objects. In plasma globes and lightning bolts, their paths are illuminated, tracing luminous arcs through space. The chemical identities of elements, the compounds they form, and their reactivity all hinge on electron properties. Any change in electron mass or charge would recalibrate chemistry entirely. Heavier electrons would condense atoms, demanding more energetic bonds, potentially nullifying chemical bonding. Excessively light electrons, conversely, would weaken bonds, destabilizing vital molecules like proteins and DNA, and turning benign radiation into harmful energy, capable of damaging our very genetic code.
The precise mass of electrons, their comparative lightness to protons and neutrons, is no mere happenstance—it is a prerequisite for the rich chemistry that supports life. Stephen Hawking, in "A Brief History of Time," contemplates the fundamental numbers that govern scientific laws, including the electron's charge and its mass ratio to protons. These constants appear finely tuned, fostering a universe where stars can burn and life can emerge. The proton-neutron mass relationship also plays a crucial part. They are nearly equal in mass yet distinct enough to prevent universal instability. The slightly greater mass of neutrons than protons ensures the balance necessary for the complex atomic arrangements that give rise to life. Adding to the fundamental nature of electrons, Niels Bohr's early 20th-century quantization rule stipulates that electrons occupy specific orbits, preserving atomic stability and the diversity of elements. And the Pauli Exclusion Principle, as noted by physicist Freeman Dyson, dictates that no two fermions (particles with half-integer spins like electrons) share the same quantum state, allowing only two electrons per orbital and preventing a collapse into a chemically inert universe. These laws—the quantization of electron orbits and the Pauli Exclusion Principle—form the bedrock of the complex chemistry that underpins life. Without them, our universe would be a vastly different, likely lifeless, expanse. Together, they compose a symphony of physical principles that not only allow the existence of life but also enable the myriad forms it takes.
The diverse array of atomic bonds, all rooted in electron interactions, is essential for the formation of complex matter. Without these bonds, the universe would be devoid of molecules, liquids, and solids, consisting solely of monatomic gases. Five main types of atomic bonds exist, and their strengths are influenced by the specific elements and distances between atoms involved. The fine-tuning for atomic bonds involves precise physical constants and forces in the universe, such as electromagnetic force and the specific properties of electrons. These elements must be finely balanced for atoms to interact and form stable bonds, enabling the complexity of matter. Chemical reactions hinge on the formation and disruption of chemical bonds, which essentially involve electron interactions. Without the capability of electrons to create breakable bonds, chemical reactions wouldn't occur. These reactions, which can be seen as electron transfers involving energy shifts, underpin processes like digestion, photosynthesis, and combustion, extending to industrial applications in making glues, paints, and batteries. In photosynthesis, specifically, electrons energized by light photons are transferred between molecules, facilitating ATP production in chloroplasts.
Electricity involves electron movement through conductors, facilitating energy transfer between locations, like from a battery to a light bulb. Light is generated when charged particles like electrons accelerate, emitting electromagnetic radiation without losing energy in atomic orbits.
For the universe to form galaxies, stars, and planets, the balance between electrons and protons must be incredibly precise, to a margin of one part in 10^37. This level of accuracy underscores the fine-tuning necessary for the structure of the cosmos, a concept challenging to grasp due to the vastness of the number involved. To illustrate the precision of one part in 10^37, consider filling the entire United States with coins to a depth of about 1 km. If only one of those coins is painted red, finding it on your first try with your eyes closed represents the level of precision required for the balance between electrons and protons in the universe. The precise mechanisms behind this equilibrium involve fundamental forces and principles of quantum mechanics, suggesting a highly fine-tuned process in the early universe. The precise balance of electrons and protons wasn't due to physical necessity but rather a result of the conditions and laws governing the early universe.
Last edited by Otangelo on Mon 22 Apr 2024 - 17:57; edited 17 times in total