The fascinating world of Quantum Mechanics
David Tong: Applications of Quantum Mechanics 2017
Particles in a Magnetic Field: the electric field E(x, t) and magnetic field B(x, t) can be written in terms a scalar potential φ(x, t) a and a vector potential A(x, t) b. Both φ and A are referred to as gauge fields.
Electron Dynamics in Solids
Lets get a feel of the basic properties of materials. There is one feature in particular that will be important: materials don’t just have one electron sitting in them. They have lots. A large part of condensed matter physics is concerned with in understanding the collective behaviour of this swarm of electrons.
Fermi Surfaces
Even in the absence of any interactions, electrons still are still affected by the presence of others. This is because electrons are fermions, and so subject to the Pauli exclusion principle. This is the statement that only one electron can sit in any given state. The Pauli exclusion principle, coupled with the general features of band structure, goes some way towards explaining the main properties of materials.
Phonons
In materials, atoms can jiggle, oscillating back and forth about their equilibrium position. The result of their collective effort is what we call sound waves or, at the quantum level, phonons.
Above is a simple one-dimensional lattice consisting of N equally spaced, identical atoms, each of mass . with a the lattice spacing.
A coarse grained description of atomic vibrations can be described in terms of a continuous field. The second is that quantisation of the field results in particles that, in the present context, we call phonons. There is a very important lesson to take from the second of these ideas, a lesson which extends well beyond the study of solids. All of the fundamental particles that we know of in Nature – whether electrons, quarks, photons, or anything else — arise from the quantisation of an underlying field. There is no experimental evidence that the fundamental fields in our Universe have a discrete underpinning. But at the theoretical level, there are some deep mathematical reasons — to do with chiral fermions and topology — which suggest that it is not possible to find a discrete system from which the known laws of physics emerge. It would appear that our Universe does not have something akin to the atomic lattice which underlies the phonon field.
http://www.damtp.cam.ac.uk/user/tong/aqm/aqm.pdf
a Scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location.
https://en.wikipedia.org/wiki/Scalar_potential
b Magnetic vector potential, A, is the vector quantity in classical electromagnetism defined so that its curl is equal to the magnetic field:
. Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well
https://en.wikipedia.org/wiki/Magnetic_vector_potential
In vector calculus, the curl is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.
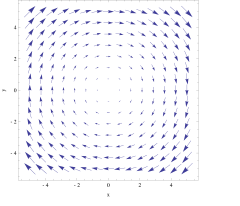
https://en.wikipedia.org/wiki/Curl_(mathematics)
http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/parcon.html
David Tong: Applications of Quantum Mechanics 2017
Particles in a Magnetic Field: the electric field E(x, t) and magnetic field B(x, t) can be written in terms a scalar potential φ(x, t) a and a vector potential A(x, t) b. Both φ and A are referred to as gauge fields.
Electron Dynamics in Solids
Lets get a feel of the basic properties of materials. There is one feature in particular that will be important: materials don’t just have one electron sitting in them. They have lots. A large part of condensed matter physics is concerned with in understanding the collective behaviour of this swarm of electrons.
Fermi Surfaces
Even in the absence of any interactions, electrons still are still affected by the presence of others. This is because electrons are fermions, and so subject to the Pauli exclusion principle. This is the statement that only one electron can sit in any given state. The Pauli exclusion principle, coupled with the general features of band structure, goes some way towards explaining the main properties of materials.
Phonons
In materials, atoms can jiggle, oscillating back and forth about their equilibrium position. The result of their collective effort is what we call sound waves or, at the quantum level, phonons.
Above is a simple one-dimensional lattice consisting of N equally spaced, identical atoms, each of mass . with a the lattice spacing.
A coarse grained description of atomic vibrations can be described in terms of a continuous field. The second is that quantisation of the field results in particles that, in the present context, we call phonons. There is a very important lesson to take from the second of these ideas, a lesson which extends well beyond the study of solids. All of the fundamental particles that we know of in Nature – whether electrons, quarks, photons, or anything else — arise from the quantisation of an underlying field. There is no experimental evidence that the fundamental fields in our Universe have a discrete underpinning. But at the theoretical level, there are some deep mathematical reasons — to do with chiral fermions and topology — which suggest that it is not possible to find a discrete system from which the known laws of physics emerge. It would appear that our Universe does not have something akin to the atomic lattice which underlies the phonon field.
http://www.damtp.cam.ac.uk/user/tong/aqm/aqm.pdf
a Scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location.
https://en.wikipedia.org/wiki/Scalar_potential
b Magnetic vector potential, A, is the vector quantity in classical electromagnetism defined so that its curl is equal to the magnetic field:
. Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as wellhttps://en.wikipedia.org/wiki/Magnetic_vector_potential
In vector calculus, the curl is a vector operator that describes the infinitesimal circulation of a vector field in three-dimensional Euclidean space. The curl at a point in the field is represented by a vector whose length and direction denote the magnitude and axis of the maximum circulation. The curl of a field is formally defined as the circulation density at each point of the field.
https://en.wikipedia.org/wiki/Curl_(mathematics)
http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/parcon.html
