Fine-tuning of the physical constants
https://reasonandscience.catsboard.com/t3134-fine-tuning-of-the-physical-constants#8607
Fine-tuning of the physical constants is evidence of design
1. Time, length, mass, electric current, temperature, amount of substance, and luminous intensity are fundamental properties and the most basic ones of the cosmos, and our world. They are themselves ungrounded and they ground all of the other things. They are not calculable from even deeper principles currently known. The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. An example of a fundamental constant is Newton’s gravitational constant G, which determines the strength of gravity via Newton’s law.
2. These constants have a fixed value, and they are just right to permit a life-permitting universe. Many of the fundamental physical constants could have any value, there are no constraints on the possible values that any of the constants can take. So the alternative values are infinite.
3. They are in fact very precise adjusted or fine-tuned, to produce the only kind of Universe that makes our existence possible. The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life. Evidence supports the conclusion that they were adjusted by a fine-tuner.
Time, length, mass, electric current, temperature, amount of substance, and luminous intensity are fundamental properties of the cosmos and the most basic ones of our world. They are themselves ungrounded and they ground all of the other things. So you cannot dig deeper. Now here is the thing: These properties are fundamental constants that are like the DNA of our Universe. They are not calculable from even deeper principles currently known. The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. An example of a fundamental constant is Newton’s gravitational constant G, which determines the strength of gravity via Newton’s law.
These constants have a fixed value, and they are just right to permit a life-permitting universe. For life to emerge in our Universe the fundamental constants could not have been more than a fraction of a percent from their actual values. Many of the fundamental physical constants could have any value, so the alternative values are infinite. The BIG question is: Why is that so? These constants can’t be derived from other constants and have to be verified by experiment. Simply put: Science has no answer and does not know why they have the value that they have.
An example is the mass of the fundamental particles, like quark masses which define the mass of protons, neutrons, etc. There would be almost an infinite number of possible combinations of quarks, but if protons had other combinations, there would be no stable atoms, and we would not be here. The Standard Model of particle physics alone contains 26 such free parameters. It contains both coupling constants and particle masses.
They are in fact very precise adjusted or fine-tuned, to produce the only kind of Universe that makes our existence possible. The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life. There are no constraints on the possible values that any of the constants can take.
Observation:
Fundamental properties are the most basic properties of a world. In terms of the notion of grounding, fundamental properties are themselves ungrounded and they (at least partially) ground all of the other properties. The laws metaphysically determine what happens in the worlds that they govern. These laws have a metaphysically objective existence. Laws systematize the world.
Question:
What are the fundamental laws of nature/physics, and the constants, that govern the physical world? If these laws are necessary, and the constants require a specific value in a narrow range for a life-permitting universe to exist, why is the universe set to be life-permitting, rather than not?
Given our restricted focus, naturalism is non-informative with respect to the fundamental constants. Naturalism gives us no reason to expect physical reality to be one way rather than some other way, at the level of its ultimate laws. This is because there are no true principles of reality that are deeper than the ultimate laws. There just isn’t anything that could possibly provide such a reason. The only non-physical constraint is mathematical consistency.
There are many constants that cannot be predicted, just measured. That means, the specific numbers in the mathematical equations that define the laws of physics cannot be derived from more fundamental things. They are just what they are, without further explanation. Why is that so? Nobody knows. What we do know, however, is, that if these numbers in the equations would be different, we would not be here. An example is the mass of the fundamental particles, like quark masses which define the mass of protons, neutrons, etc. There would be almost an infinite number of possible combinations of quarks, but if protons had other combinations, there would be no stable atoms, and we would not be here.
The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. Constants whose value can be deduced from other deeper facts about physics and math are called derived constants. A fundamental constant, often called a free parameter, is a quantity whose numerical value can’t be determined by any computations. In this regard, it is the lowest building block of equations as these quantities have to be determined experimentally. When talking about fine-tuning we are talking about constants can’t be derived from other constants and have to be verified by experiment. Simply put: we don’t know why they have that value. The Standard Model of particle physics alone contains 26 such free parameters. It contains both coupling constants and particle masses. Many of the fundamental physical constants, God could have given any value He liked-are in fact very precised adjusted, or fine-tuned, to produce the only kind of Universe that makes our existence possible. The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life. There are no constraints on the possible values that any of the constants can take.
Although they represent a significant problem for particle physics theories, the observed hierarchies of the fundamental parameters are a distinguishing feature of the cosmos, and extreme hierarchies are required for any universe to be viable: The strength of gravity can vary over several orders of magnitude, but it must remain weak compared to other forces so that the universe can evolve and produce structure, and stars can function. This required weakness of gravity leads to the hierarchies of scale that we observe in the universe. In addition, any working universe requires a clean separation of the energies corresponding to the vacuum, atoms, nuclei, electroweak symmetry breaking, and the Planck scale. In other words, the hierarchies of physics lead to the observed hierarchies of astrophysics, and this ordering is necessary for a habitable universe. The universe is surprisingly resilient to changes in its fundamental and cosmological parameters.
One notworthy thing in theoretical physics is the hierarchy problem, concerning the large discrepancy between aspects of the weak force and gravity. There is no scientific explanation on why, for example, the weak force is 10^24 times stronger than gravity. Suppose a physics model requires four parameters which allow it to produce a very high-quality working model, generating predictions of some aspect of our physical universe. Suppose we find through experiments that the parameters have values:
1.2
1.31
0.9 and
40433155790211602455360270321658, 8 (roughly 4×10^29).
We might wonder how such figures arise. But in particular, we might be especially curious about a theory where three values are close to one, and the fourth is so different; in other words, the huge disproportion we seem to find between the first three parameters and the fourth. We might also wonder, if one force is so much weaker than the others that it needs a factor of 4×10^29 to allow it to be related to them in terms of effects, how did our universe come to be so exactly balanced when its forces emerged? In current particle physics, the differences between some parameters are much larger than this, so the question is even more noteworthy.
Wikipedia: Dimensionless physical constant
In physics, a dimensionless physical constant is a physical constant that is dimensionless, i.e. a pure number having no units attached and having a numerical value that is independent of whatever system of units may be used. The term fundamental physical constant has been sometimes used to refer to certain universal dimensioned physical constants, such as the speed of light c, vacuum permittivity ε0, Planck constant h, and the gravitational constant G, that appear in the most basic theories of physics.
https://en.wikipedia.org/wiki/Dimensionless_physical_constant
CODATA RECOMMENDED VALUES OF THE FUNDAMENTAL PHYSICAL CONSTANTS: 2018
https://physics.nist.gov/cuu/pdf/wall_2018.pdf
“Many of the fundamental physical constants-which as far as one could see, God could have given any value He liked-are in fact very precised adjusted, or fine-tuned, to produce the only kind of Universe that makes our existence possible.” — Arthur C. Clarke
The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life.
ROBIN COLLINS The Teleological Argument: An Exploration of the Fine-Tuning of the Universe 2009
The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. An example of a fundamental constant is Newton’s gravitational constant G, which determines the strength of gravity via Newton’s law. We will say that a constant is fine-tuned if the width of its life-permitting range, Wr, is very small in comparison to the width, WR, of some properly chosen comparison range: that is, Wr/WR << 1.
Fine-tuning of gravity
Using a standard measure of force strengths – which turns out to be roughly the relative strength of the various forces between two protons in a nucleus – gravity is the weakest of the forces, and the strong nuclear force is the strongest, being a factor of 10^40 – or 10 thousand billion, billion, billion, billion times stronger than gravity. Now if we increased the strength of gravity a billionfold, for instance, the force of gravity on a planet with the mass and size of the Earth would be so great that organisms anywhere near the size of human beings, whether land-based or aquatic, would be crushed. (The strength of materials depends on the electromagnetic force via the fine-structure constant, which would not be affected by a change in gravity.) Even a much smaller planet of only 40 ft in diameter – which is not large enough to sustain organisms of our size – would have a gravitational pull of 1,000 times that of Earth, still too strong for organisms of our size to exist. As astrophysicist Martin Rees notes, “In an imaginary strong gravity world, even insects would need thick legs to support them, and no animals could get much larger”. Consequently, such an increase in the strength of gravity would render the existence of embodied life virtually impossible and thus would not be life-permitting in the sense that we defined. Of course, a billionfold increase in the strength of gravity is a lot, but compared with the total range of the strengths of the forces in nature (which span a range of 10^40), it is very small, being one part in 10 thousand, billion, billion, billion. Indeed, other calculations show that stars with lifetimes of more than a billion years, as compared with our Sun’s lifetime of 10 billion years, could not exist if gravity were increased by more than a factor of 3,000. This would significantly inhibit the occurrence of embodied life. The case of fine-tuning of gravity described is relative to the strength of the electromagnetic force, since it is this force that determines the strength of materials – for example, how much weight an insect leg can hold; it is also indirectly relative to other constants – such as the speed of light, the electron and proton mass, and the like – which help determine the properties of matter. There is, however, a fine-tuning of gravity relative to other parameters. One of these is the fine-tuning of gravity relative to the density of mass-energy in the early universe and other factors determining the expansion rate of the Big Bang – such as the value of the Hubble constant and the value of the cosmological constant. Holding these other parameters constant, if the strength of gravity were smaller or larger by an estimated one part in 10^60 of its current value, the universe would have either exploded too quickly for galaxies and stars to form, or collapsed back on itself too quickly for life to evolve. The lesson here is that a single parameter, such as gravity, participates in several different fine-tunings relative to other parameters.
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.696.63&rep=rep1&type=pdf
Julian De Vuyst: A Natural Introduction to Fine-Tuning 10 Dec 2020 4
Derived vs Fundamental Constants
There is a subdivision within constants that is related to how their value is determined. Constants whose value can be deduced from other deeper facts about physics and math are called derived constants. Such constants include π which is derived from the ratio of the circumference of a circle and its radius and g which can be derived from Newton’s gravitational law close to the Earth’s surface. Note that, while there are literally dozens of ways to calculate π, its numerical value does not depend on other constants. This is in contrast with g whose value depends on the radius of the Earth, it's mass, and Newton’s constant. In the other case, a fundamental constant, often called a free parameter, is a quantity whose numerical value can’t be determined by any computations. In this regard, it is the lowest building block of equations as these quantities have to be determined experimentally. The Standard Model alone contains 26 such free parameters
• The twelve fermion masses/Yukawa couplings to the Higgs field;
• The three coupling constants of the electromagnetic, weak, and strong interactions;
• The vacuum expectation value and mass of the Higgs boson3 ;
• The eight mixing angles of the PMNS and CKM matrices;
• The strong CP phase related to the strong CP problem.
Other free parameters include Newton’s constant, the cosmological constant, etc.
When talking about naturalness and fine-tuning we are talking about dimensionless6 and fundamental constants, because
1. These are the constants with a fixed value regardless of the model we are considering and therefore have significance;
2. These constants can’t be derived from other constants and have to be verified by experiment. Simply put: we don’t know why they have that value.
P. Davies describes the Goldilocks Principle: for life to emerge in our Universe the fundamental constants could not have been more than a few percent from their actual values. For instance, for elements as complex as carbon to be stable, the electron-proton mass ratio me/mp = 5.45 · 10−4 and the fine-structure α = 7.30 · 10−3 may not have values differing greatly from these.
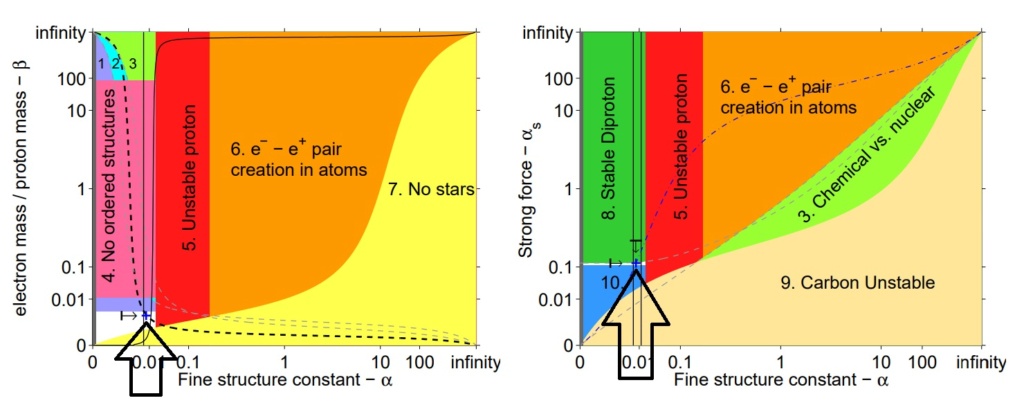
The life-permitting region (shown in white) in the (α, β) (left) and (α, αs) (right) parameter space, with other constants held at their values in our universe. Our universe is shown as a blue cross.
They are just about right. The study of such relations is referred to as anthropic fine-tuning: the quantification of how much these parameters in our theories could be changed so that life as we know it would still be possible . As we will see, this leads to the design argument and anthropic principle as possible solutions. Life as we know it is carbon-based, we have yet to encounter another species with different properties of fulfilling what life is according to their inner workings. Universes with different constants would give rise to less structure and complexity. This would make such Universes life-hostile.
The Cosmological Constant Problem
Observations concluded that the Universe at cosmological scales, at the scale of galaxy clusters, is homogeneous and isotropic. Furthermore, the Universe seems to be in an era of expansion (first noted by Hubble and Lemaitre). In order to obtain an expanding Universe, one can add the cosmological constant. It turns out that when we apply quantum field theory to compute the vacuum energy contribution, the theoretically obtained value and the experimentally observed one differ by 121 orders of magnitude. Even when one takes supersymmetry to be true, the difference still remains at about 80 orders of magnitude.
The Flatness Problem
It is well-known that our expanding Universe can be well described by a Friedmann-LemaˆıtreRobertson-Walker metric which is the general metric for an isotropic, homogeneous expanding Universe. Our Universe today is very flat, meaning that k = 0, hence from the equation follows that Ω today is very close to 1. Using some algebraic manipulations one can compute what Ω was in the early Universe. It turns out that to have Ω = 1 today, Ωearly must also lie extremely close to 1. This fine-tuning of Ωearly is called the Flatness Problem. This problem is what inflation theory solves.
The Higgs Mass
The Higgs boson, only just recently discovered, plays an important role in the Standard Model: it is the only scalar field (spin = 0) and the coupling to this boson is responsible for a part of the mass of the elementary particles. To keep the Higgs mass within the observed range one hence requires large cancellations among each other in the loop corrections effectively introducing a new term which almost exactly cancels the loop term to a high degree of precision. This is no problem as this new term is not observable and the current value of the Higgs mass agrees well with predictions and measurements. This is dubbed the Hierarchy Problem since these extra terms need to be fine-tuned. A popular solution to this problem is supersymmetry: the statement that each particle in the Standard Model has a superpartner called an sparticle. These new sparticles can introduce new loops effectively countering the original large contributions. Yet, as these loops depend on the masses of these sparticles, any sparticles with a mass higher than the Higgs mass would reintroduce the problem. The problem is hence shifted from arbitrarily precise loop cancellations to the masses of these sparticles. However, there is currently no experimental evidence for supersymmetry.
The Strong CP Problem
For any quantum field theory to be consistent, it must be symmetric under the combined action of CPT:
1. C-symmetry (charge conjugation)
2. P-symmetry (parity)
3. T-symmetry (time reversal)
Designed like Clockwork
Just like the intricate workings of a watch, could the Universe and its finely tuned constants also be created by some metaphysical entity who certainly did know his physics?
Many physical constants must lie in an extremely narrow range, in order for life to exist. Currently, we have no explanation why certain physical constants have the exact values that permit life, in special considering, that each value in the possible ranges is equally likely. There are no constraints on the possible values that any of the constants can take. The probability of having life permitting constants is vanishingly small. Very improbable, not theoretically impossible, because it is not exactly 0. Nonetheless, when the probability is less than one positive outcome in a range of more than 1^50 according to Borel's law, we can conclude that a certain event is impossible to occur by chance.
When thinking about the design argument, it mostly goes something like this
1. Our Universe seems remarkably fine-tuned for the emergence of carbon-based life;
2. The boundary conditions and laws of physics could not have differed too much from the way they are in order for the Universe to contain life;
3. Our Universe does contain life. Therefore 1. Our Universe is improbable; 2. “Our Universe is created by some intelligent being” is the best explanation. Such that 1. A Universe-creating intelligent entity exists.
As someone who does not believe in metaphysical beings, I don’t adhere to this solution. Throughout history, we have seen that more and more phenomena that were first being described as ‘divine intervention’ made way for a natural, physical explanation. I think it would be more likely that the fine-tuning problem can also be solved without invoking a metaphysical reality. But, the difficulty of this problem should not be underestimated. If their is indeed a universal mathematical structure as stated by Tegmark then the fine-tuning problem should be explained by this theory. It seems like every try to analyze the problem using probability theory either fails or shifts the question. Even then, the probability for our Universe to have constants with those values remains very low. Naturally, it hence seems counterintuitive to believe this solution. That we are simply the ‘lucky ones’, mainly because the probability is itself very counterintuitive. To be honest, it is a very displeasing proposal. In the end, it seems like opting for this proposal is the same as abandoning the search for an explanation. Somehow, I do find this more compelling than the anthropic principle and design argument, though.
My comment: This is a remarkable confession. The author prefers, rather than to permit the evidence to lead to the best, case-adequate explanation, to stick to his a priori decided & adopted worldview, no matter if the evidence points to another direction. The next claim is based on no evidence: Never has there been a compelling explanation of natural phenomena based on alternative mechanisms to design. In the end, he sticks to a classical " Naturalism of the gaps" argument, invoking natural explanations which have not been discovered yet.
Fred C. Adams: The Degree of Fine-Tuning in our Universe – and Others 11 Feb 2019
Within our universe, the laws of physics have the proper form to support all of the building blocks that are needed for observers to arise. However, a large and growing body of research has argued that relatively small changes in the laws of physics could render the universe incapable of supporting life. In other words, the universe could be fine-tuned for the development of complexity. The list of required structures to have a life-permitting universe includes complex nuclei, planets, stars, galaxies, and the universe itself. In addition to their existence, these structures must have the right properties to support observers. Stable nuclei must populate an adequate fraction of the periodic table. Stars must be sufficiently hot and live for a long time. The galaxies must have gravitational potential wells that are deep enough to retain heavy elements produced by stars and not overly dense so that planets can remain in orbit. The universe itself must allow galaxies to form and live long enough for complexity to arise.
In order to make a full assessment of the degree of fine-tuning of the universe, one must address the following components of the problem:
I Specification of the relevant parameters of physics and astrophysics that can vary.
II Determination of the allowed ranges of parameters that allow for the development of complexity and hence observers.
III Identification of the underlying probability distributions from which the fundamental parameters are drawn, including the full possible range that the parameters can take.
IV Consideration of selection effects that allow the interpretation of observed properties in the context of the a priori probability distributions.
V Synthesis of the preceding ingredients to determine the overall likelihood for universes to become habitable
Studying the degree of tuning necessary for the universe to operate provides us with a greater understanding of how it works.
Both the fundamental constants that describe the laws of physics and the cosmological parameters that determine the properties of our universe must fall within a range of values in order for the cosmos to develop astrophysical structures and ultimately support life. 1 y. The standard model of particle physics contains both coupling constants a and particle masses.
The cosmological parameters, including
- the total energy density of the universe (Ω),
- the contribution from vacuum energy (ρΛ),
- the baryon-to-photon ratio (η),
- the dark matter contribution (δ),
- the amplitude of primordial density fluctuations (Q).
are quantities that are constrained by the requirements that the universe lives for a sufficiently long time emerges from the epoch of Big Bang Nucleosynthesis with an acceptable chemical composition, and can successfully produce large-scale structures such as galaxies. On smaller scales, stars and planets must be able to form and function. The stars must be sufficiently long-lived, have high enough surface temperatures, and have smaller masses than their host galaxies. The planets must be massive enough to hold onto an atmosphere, yet small enough to remain non-degenerate, and contain enough particles to support a biosphere of sufficient complexity. These requirements place constraints on
- the gravitational structure constant (αG),
- the fine structure constant (α),
- composite parameters (C?)
that specify nuclear reaction rates. Specific instances also require the fine-tuning in stellar nucleosynthesis, including the triple-alpha reaction that produces carbon. A fundamental question thus arises: What versions of the laws of physics are necessary for the development of astrophysical structures, which are in turn necessary for the development of life?
Physical Constants The progress of physics has revealed a host of physical constants, all of which have been measured to varying degrees of precision – for example, the speed of light (c), Planck’s constant (h¯), the gravitational constant (G), the charge of the electron (e), and the masses of various elementary particles like the proton (mp) and the electron (me). As physics has become progressively unified, the number of fundamental constants has reduced, but there is still a large number of them. The Standard Model of Particle Physics has 26, and the Standard Model of Cosmology has six constants.
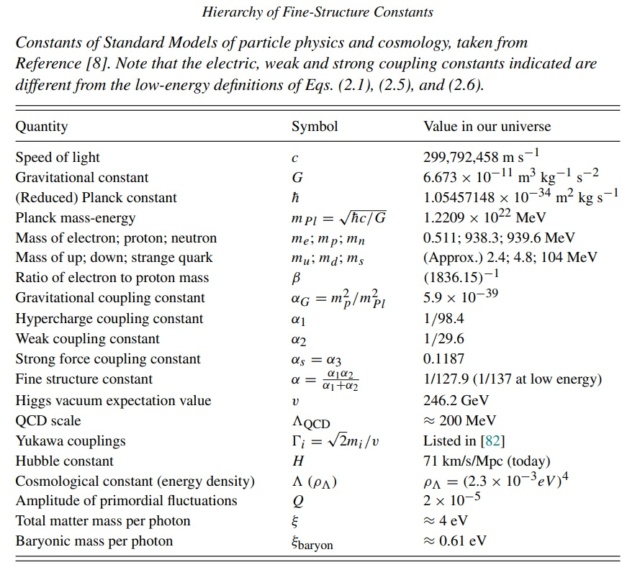
It is well known that the Standard Model of Particle Physics has at least 26 parameters, but the theory must be extended to account for additional physics, including gravity, neutrino oscillations, dark matter, and dark energy
Cosmological Parameters and the Cosmic Inventory
A set of cosmological parameters are necessary to specify the current state of our universe. The current state of the universe can be characterized by a relatively small collection of parameters. The expansion of the universe is governed by the Friedmann equation. If we are concerned only with the expansion and evolution of the universe as a whole — and not the formation of structure within it — then the current state of the universe can be specified by measuring all of the contributions to the energy density ρ and the Hubble constant.

Table of the observed cosmological parameters in our universe.
These quantities have been measured by a number of cosmological experiments. The values are listed with few enough significant digits that they are consistent with all current measurements.
For our universe, the full range of allowed energy/time/mass scales spans a factor of ∼ 10^61. Similarly, the range of mass and size scales allowed by physical considerations span about 80^15. . If the parameter probabilities were distributed evenly in logarithmic space across a comparable range (of order 100 decades — see also the discussion below), then the allowed ranges of parameter space correspond to a few percent (maybe ∼ 1 − 10%) of the total. In contrast, if the parameters were distributed uniformly over the full range — and the viable parameters do not lie at the upper end of that range — then the allowed range would represent an incredibly small fraction of the total.
Although they represent a significant problem for particle physics theories, the observed hierarchies of the fundamental parameters are a distinguishing feature of the cosmos, and extreme hierarchies are required for any universe to be viable: The strength of gravity can vary over several orders of magnitude, but it must remain weak compared to other forces so that the universe can evolve and produce structure, and stars can function. This required weakness of gravity leads to the hierarchies of scale that we observe in the universe. In addition, any working universe requires a clean separation of the energies corresponding to the vacuum, atoms, nuclei, electroweak symmetry breaking, and the Planck scale. In other words, the hierarchies of physics lead to the observed hierarchies of astrophysics, and this ordering is necessary for a habitable universe. The universe is surprisingly resilient to changes in its fundamental and cosmological parameters.
Robin Collins: The Argument from Physical Constants: The Fine-Tuning for Discoverability 3
The Higgs boson is a key particle of our most fundamental model of particle physics, called the Standard Model (SM). The SM is the most fundamental physical model regarding the ultimate structure of matter. It is generally thought to be incomplete, a low-energy approximation to a deeper theory; in the forty years since its existence, however, it has withstood every test. It consists of a set of elementary particles and laws governing their interactions. These particles are the quarks and leptons; the particles that carry the electromagnetic, weak, and strong forces (called the gauge bosons); and the recently discovered Higgs boson. Quarks and leptons come in generations. The particles in a given row are identical except for their mass, with the mass of the particles increases with each generation: for example, the charm quark is about 500 times more massive than the up quark, and the top quark is about 130 times as massive as the charm quark. Only the first generation plays a direct role in life. Specifically, atoms are composed of electrons orbiting a nucleus composed of protons and neutrons, with the protons being composed of two up quarks and one down quark, and the neutron is composed of two down quarks and one up quark. Even though protons and neutrons are made of quarks, most of their mass does not come from the quarks but from the strong force that binds the quarks together.
Casey Luskin: The Fine-Tuning of the Universe November 8, 2017 2
The following gives a sense of the degree of fine-tuning that must go into some of these values to yield a life-friendly universe:
Gravitational constant: 1 part in 10^34
Electromagnetic force versus force of gravity: 1 part in 10^37
Cosmological constant: 1 part in 10^120
Mass density of universe: 1 part in 10^59
Expansion rate of universe: 1 part in 10^55
Initial entropy: 1 part in 10^ (10^123)
The last item in the list — the initial entropy of the universe — shows an astounding degree of fine-tuning.
Paul Davies's book The Goldilocks Enigma (2006) reviews the current state of the fine tuning debate in detail, and concludes by enumerating the following responses to that debate:
The absurd universe: Our universe just happens to be the way it is.
The unique universe: There is a deep underlying unity in physics that necessitates the Universe being the way it is. Some Theory of Everything will explain why the various features of the Universe must have exactly the values that we see.
The multiverse: Multiple universes exist, having all possible combinations of characteristics, and we inevitably find ourselves within a universe that allows us to exist.
Intelligent design: A creator designed the Universe with the purpose of supporting complexity and the emergence of intelligence.
The life principle: There is an underlying principle that constrains the Universe to evolve towards life and mind.
The self-explaining universe: A closed explanatory or causal loop: "perhaps only universes with a capacity for consciousness can exist". This is Wheeler's Participatory Anthropic Principle (PAP).
The fake universe: We live inside a virtual reality simulation.
a: In physics, a coupling constant or gauge coupling parameter (or, more simply, a coupling), is a number that determines the strength of the force exerted in an interaction.
1. https://arxiv.org/pdf/1902.03928.pdf
2. https://evolutionnews.org/2017/11/ids-top-six-the-fine-tuning-of-the-universe/
3. http://library.lol/main/643DEBF15D83B06F4AD0F574F37883FA
4. https://arxiv.org/pdf/2012.05617.pdf

https://reasonandscience.catsboard.com/t3134-fine-tuning-of-the-physical-constants#8607
Fine-tuning of the physical constants is evidence of design
1. Time, length, mass, electric current, temperature, amount of substance, and luminous intensity are fundamental properties and the most basic ones of the cosmos, and our world. They are themselves ungrounded and they ground all of the other things. They are not calculable from even deeper principles currently known. The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. An example of a fundamental constant is Newton’s gravitational constant G, which determines the strength of gravity via Newton’s law.
2. These constants have a fixed value, and they are just right to permit a life-permitting universe. Many of the fundamental physical constants could have any value, there are no constraints on the possible values that any of the constants can take. So the alternative values are infinite.
3. They are in fact very precise adjusted or fine-tuned, to produce the only kind of Universe that makes our existence possible. The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life. Evidence supports the conclusion that they were adjusted by a fine-tuner.
Time, length, mass, electric current, temperature, amount of substance, and luminous intensity are fundamental properties of the cosmos and the most basic ones of our world. They are themselves ungrounded and they ground all of the other things. So you cannot dig deeper. Now here is the thing: These properties are fundamental constants that are like the DNA of our Universe. They are not calculable from even deeper principles currently known. The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. An example of a fundamental constant is Newton’s gravitational constant G, which determines the strength of gravity via Newton’s law.
These constants have a fixed value, and they are just right to permit a life-permitting universe. For life to emerge in our Universe the fundamental constants could not have been more than a fraction of a percent from their actual values. Many of the fundamental physical constants could have any value, so the alternative values are infinite. The BIG question is: Why is that so? These constants can’t be derived from other constants and have to be verified by experiment. Simply put: Science has no answer and does not know why they have the value that they have.
An example is the mass of the fundamental particles, like quark masses which define the mass of protons, neutrons, etc. There would be almost an infinite number of possible combinations of quarks, but if protons had other combinations, there would be no stable atoms, and we would not be here. The Standard Model of particle physics alone contains 26 such free parameters. It contains both coupling constants and particle masses.
They are in fact very precise adjusted or fine-tuned, to produce the only kind of Universe that makes our existence possible. The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life. There are no constraints on the possible values that any of the constants can take.
Observation:
Fundamental properties are the most basic properties of a world. In terms of the notion of grounding, fundamental properties are themselves ungrounded and they (at least partially) ground all of the other properties. The laws metaphysically determine what happens in the worlds that they govern. These laws have a metaphysically objective existence. Laws systematize the world.
Question:
What are the fundamental laws of nature/physics, and the constants, that govern the physical world? If these laws are necessary, and the constants require a specific value in a narrow range for a life-permitting universe to exist, why is the universe set to be life-permitting, rather than not?
Given our restricted focus, naturalism is non-informative with respect to the fundamental constants. Naturalism gives us no reason to expect physical reality to be one way rather than some other way, at the level of its ultimate laws. This is because there are no true principles of reality that are deeper than the ultimate laws. There just isn’t anything that could possibly provide such a reason. The only non-physical constraint is mathematical consistency.
There are many constants that cannot be predicted, just measured. That means, the specific numbers in the mathematical equations that define the laws of physics cannot be derived from more fundamental things. They are just what they are, without further explanation. Why is that so? Nobody knows. What we do know, however, is, that if these numbers in the equations would be different, we would not be here. An example is the mass of the fundamental particles, like quark masses which define the mass of protons, neutrons, etc. There would be almost an infinite number of possible combinations of quarks, but if protons had other combinations, there would be no stable atoms, and we would not be here.
The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. Constants whose value can be deduced from other deeper facts about physics and math are called derived constants. A fundamental constant, often called a free parameter, is a quantity whose numerical value can’t be determined by any computations. In this regard, it is the lowest building block of equations as these quantities have to be determined experimentally. When talking about fine-tuning we are talking about constants can’t be derived from other constants and have to be verified by experiment. Simply put: we don’t know why they have that value. The Standard Model of particle physics alone contains 26 such free parameters. It contains both coupling constants and particle masses. Many of the fundamental physical constants, God could have given any value He liked-are in fact very precised adjusted, or fine-tuned, to produce the only kind of Universe that makes our existence possible. The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life. There are no constraints on the possible values that any of the constants can take.
Although they represent a significant problem for particle physics theories, the observed hierarchies of the fundamental parameters are a distinguishing feature of the cosmos, and extreme hierarchies are required for any universe to be viable: The strength of gravity can vary over several orders of magnitude, but it must remain weak compared to other forces so that the universe can evolve and produce structure, and stars can function. This required weakness of gravity leads to the hierarchies of scale that we observe in the universe. In addition, any working universe requires a clean separation of the energies corresponding to the vacuum, atoms, nuclei, electroweak symmetry breaking, and the Planck scale. In other words, the hierarchies of physics lead to the observed hierarchies of astrophysics, and this ordering is necessary for a habitable universe. The universe is surprisingly resilient to changes in its fundamental and cosmological parameters.
One notworthy thing in theoretical physics is the hierarchy problem, concerning the large discrepancy between aspects of the weak force and gravity. There is no scientific explanation on why, for example, the weak force is 10^24 times stronger than gravity. Suppose a physics model requires four parameters which allow it to produce a very high-quality working model, generating predictions of some aspect of our physical universe. Suppose we find through experiments that the parameters have values:
1.2
1.31
0.9 and
40433155790211602455360270321658, 8 (roughly 4×10^29).
We might wonder how such figures arise. But in particular, we might be especially curious about a theory where three values are close to one, and the fourth is so different; in other words, the huge disproportion we seem to find between the first three parameters and the fourth. We might also wonder, if one force is so much weaker than the others that it needs a factor of 4×10^29 to allow it to be related to them in terms of effects, how did our universe come to be so exactly balanced when its forces emerged? In current particle physics, the differences between some parameters are much larger than this, so the question is even more noteworthy.
Wikipedia: Dimensionless physical constant
In physics, a dimensionless physical constant is a physical constant that is dimensionless, i.e. a pure number having no units attached and having a numerical value that is independent of whatever system of units may be used. The term fundamental physical constant has been sometimes used to refer to certain universal dimensioned physical constants, such as the speed of light c, vacuum permittivity ε0, Planck constant h, and the gravitational constant G, that appear in the most basic theories of physics.
https://en.wikipedia.org/wiki/Dimensionless_physical_constant
CODATA RECOMMENDED VALUES OF THE FUNDAMENTAL PHYSICAL CONSTANTS: 2018
https://physics.nist.gov/cuu/pdf/wall_2018.pdf
“Many of the fundamental physical constants-which as far as one could see, God could have given any value He liked-are in fact very precised adjusted, or fine-tuned, to produce the only kind of Universe that makes our existence possible.” — Arthur C. Clarke
The finely tuned laws and constants of the universe are an example of specified complexity in nature. They are complex in that their values and settings are highly unlikely. They are specified in that they match the specific requirements needed for life.
ROBIN COLLINS The Teleological Argument: An Exploration of the Fine-Tuning of the Universe 2009
The constants of physics are fundamental numbers that, when plugged into the laws of physics, determine the basic structure of the universe. An example of a fundamental constant is Newton’s gravitational constant G, which determines the strength of gravity via Newton’s law. We will say that a constant is fine-tuned if the width of its life-permitting range, Wr, is very small in comparison to the width, WR, of some properly chosen comparison range: that is, Wr/WR << 1.
Fine-tuning of gravity
Using a standard measure of force strengths – which turns out to be roughly the relative strength of the various forces between two protons in a nucleus – gravity is the weakest of the forces, and the strong nuclear force is the strongest, being a factor of 10^40 – or 10 thousand billion, billion, billion, billion times stronger than gravity. Now if we increased the strength of gravity a billionfold, for instance, the force of gravity on a planet with the mass and size of the Earth would be so great that organisms anywhere near the size of human beings, whether land-based or aquatic, would be crushed. (The strength of materials depends on the electromagnetic force via the fine-structure constant, which would not be affected by a change in gravity.) Even a much smaller planet of only 40 ft in diameter – which is not large enough to sustain organisms of our size – would have a gravitational pull of 1,000 times that of Earth, still too strong for organisms of our size to exist. As astrophysicist Martin Rees notes, “In an imaginary strong gravity world, even insects would need thick legs to support them, and no animals could get much larger”. Consequently, such an increase in the strength of gravity would render the existence of embodied life virtually impossible and thus would not be life-permitting in the sense that we defined. Of course, a billionfold increase in the strength of gravity is a lot, but compared with the total range of the strengths of the forces in nature (which span a range of 10^40), it is very small, being one part in 10 thousand, billion, billion, billion. Indeed, other calculations show that stars with lifetimes of more than a billion years, as compared with our Sun’s lifetime of 10 billion years, could not exist if gravity were increased by more than a factor of 3,000. This would significantly inhibit the occurrence of embodied life. The case of fine-tuning of gravity described is relative to the strength of the electromagnetic force, since it is this force that determines the strength of materials – for example, how much weight an insect leg can hold; it is also indirectly relative to other constants – such as the speed of light, the electron and proton mass, and the like – which help determine the properties of matter. There is, however, a fine-tuning of gravity relative to other parameters. One of these is the fine-tuning of gravity relative to the density of mass-energy in the early universe and other factors determining the expansion rate of the Big Bang – such as the value of the Hubble constant and the value of the cosmological constant. Holding these other parameters constant, if the strength of gravity were smaller or larger by an estimated one part in 10^60 of its current value, the universe would have either exploded too quickly for galaxies and stars to form, or collapsed back on itself too quickly for life to evolve. The lesson here is that a single parameter, such as gravity, participates in several different fine-tunings relative to other parameters.
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.696.63&rep=rep1&type=pdf
Julian De Vuyst: A Natural Introduction to Fine-Tuning 10 Dec 2020 4
Derived vs Fundamental Constants
There is a subdivision within constants that is related to how their value is determined. Constants whose value can be deduced from other deeper facts about physics and math are called derived constants. Such constants include π which is derived from the ratio of the circumference of a circle and its radius and g which can be derived from Newton’s gravitational law close to the Earth’s surface. Note that, while there are literally dozens of ways to calculate π, its numerical value does not depend on other constants. This is in contrast with g whose value depends on the radius of the Earth, it's mass, and Newton’s constant. In the other case, a fundamental constant, often called a free parameter, is a quantity whose numerical value can’t be determined by any computations. In this regard, it is the lowest building block of equations as these quantities have to be determined experimentally. The Standard Model alone contains 26 such free parameters
• The twelve fermion masses/Yukawa couplings to the Higgs field;
• The three coupling constants of the electromagnetic, weak, and strong interactions;
• The vacuum expectation value and mass of the Higgs boson3 ;
• The eight mixing angles of the PMNS and CKM matrices;
• The strong CP phase related to the strong CP problem.
Other free parameters include Newton’s constant, the cosmological constant, etc.
When talking about naturalness and fine-tuning we are talking about dimensionless6 and fundamental constants, because
1. These are the constants with a fixed value regardless of the model we are considering and therefore have significance;
2. These constants can’t be derived from other constants and have to be verified by experiment. Simply put: we don’t know why they have that value.
P. Davies describes the Goldilocks Principle: for life to emerge in our Universe the fundamental constants could not have been more than a few percent from their actual values. For instance, for elements as complex as carbon to be stable, the electron-proton mass ratio me/mp = 5.45 · 10−4 and the fine-structure α = 7.30 · 10−3 may not have values differing greatly from these.

The life-permitting region (shown in white) in the (α, β) (left) and (α, αs) (right) parameter space, with other constants held at their values in our universe. Our universe is shown as a blue cross.
They are just about right. The study of such relations is referred to as anthropic fine-tuning: the quantification of how much these parameters in our theories could be changed so that life as we know it would still be possible . As we will see, this leads to the design argument and anthropic principle as possible solutions. Life as we know it is carbon-based, we have yet to encounter another species with different properties of fulfilling what life is according to their inner workings. Universes with different constants would give rise to less structure and complexity. This would make such Universes life-hostile.
The Cosmological Constant Problem
Observations concluded that the Universe at cosmological scales, at the scale of galaxy clusters, is homogeneous and isotropic. Furthermore, the Universe seems to be in an era of expansion (first noted by Hubble and Lemaitre). In order to obtain an expanding Universe, one can add the cosmological constant. It turns out that when we apply quantum field theory to compute the vacuum energy contribution, the theoretically obtained value and the experimentally observed one differ by 121 orders of magnitude. Even when one takes supersymmetry to be true, the difference still remains at about 80 orders of magnitude.
The Flatness Problem
It is well-known that our expanding Universe can be well described by a Friedmann-LemaˆıtreRobertson-Walker metric which is the general metric for an isotropic, homogeneous expanding Universe. Our Universe today is very flat, meaning that k = 0, hence from the equation follows that Ω today is very close to 1. Using some algebraic manipulations one can compute what Ω was in the early Universe. It turns out that to have Ω = 1 today, Ωearly must also lie extremely close to 1. This fine-tuning of Ωearly is called the Flatness Problem. This problem is what inflation theory solves.
The Higgs Mass
The Higgs boson, only just recently discovered, plays an important role in the Standard Model: it is the only scalar field (spin = 0) and the coupling to this boson is responsible for a part of the mass of the elementary particles. To keep the Higgs mass within the observed range one hence requires large cancellations among each other in the loop corrections effectively introducing a new term which almost exactly cancels the loop term to a high degree of precision. This is no problem as this new term is not observable and the current value of the Higgs mass agrees well with predictions and measurements. This is dubbed the Hierarchy Problem since these extra terms need to be fine-tuned. A popular solution to this problem is supersymmetry: the statement that each particle in the Standard Model has a superpartner called an sparticle. These new sparticles can introduce new loops effectively countering the original large contributions. Yet, as these loops depend on the masses of these sparticles, any sparticles with a mass higher than the Higgs mass would reintroduce the problem. The problem is hence shifted from arbitrarily precise loop cancellations to the masses of these sparticles. However, there is currently no experimental evidence for supersymmetry.
The Strong CP Problem
For any quantum field theory to be consistent, it must be symmetric under the combined action of CPT:
1. C-symmetry (charge conjugation)
2. P-symmetry (parity)
3. T-symmetry (time reversal)
Designed like Clockwork
Just like the intricate workings of a watch, could the Universe and its finely tuned constants also be created by some metaphysical entity who certainly did know his physics?
Many physical constants must lie in an extremely narrow range, in order for life to exist. Currently, we have no explanation why certain physical constants have the exact values that permit life, in special considering, that each value in the possible ranges is equally likely. There are no constraints on the possible values that any of the constants can take. The probability of having life permitting constants is vanishingly small. Very improbable, not theoretically impossible, because it is not exactly 0. Nonetheless, when the probability is less than one positive outcome in a range of more than 1^50 according to Borel's law, we can conclude that a certain event is impossible to occur by chance.
When thinking about the design argument, it mostly goes something like this
1. Our Universe seems remarkably fine-tuned for the emergence of carbon-based life;
2. The boundary conditions and laws of physics could not have differed too much from the way they are in order for the Universe to contain life;
3. Our Universe does contain life. Therefore 1. Our Universe is improbable; 2. “Our Universe is created by some intelligent being” is the best explanation. Such that 1. A Universe-creating intelligent entity exists.
As someone who does not believe in metaphysical beings, I don’t adhere to this solution. Throughout history, we have seen that more and more phenomena that were first being described as ‘divine intervention’ made way for a natural, physical explanation. I think it would be more likely that the fine-tuning problem can also be solved without invoking a metaphysical reality. But, the difficulty of this problem should not be underestimated. If their is indeed a universal mathematical structure as stated by Tegmark then the fine-tuning problem should be explained by this theory. It seems like every try to analyze the problem using probability theory either fails or shifts the question. Even then, the probability for our Universe to have constants with those values remains very low. Naturally, it hence seems counterintuitive to believe this solution. That we are simply the ‘lucky ones’, mainly because the probability is itself very counterintuitive. To be honest, it is a very displeasing proposal. In the end, it seems like opting for this proposal is the same as abandoning the search for an explanation. Somehow, I do find this more compelling than the anthropic principle and design argument, though.
My comment: This is a remarkable confession. The author prefers, rather than to permit the evidence to lead to the best, case-adequate explanation, to stick to his a priori decided & adopted worldview, no matter if the evidence points to another direction. The next claim is based on no evidence: Never has there been a compelling explanation of natural phenomena based on alternative mechanisms to design. In the end, he sticks to a classical " Naturalism of the gaps" argument, invoking natural explanations which have not been discovered yet.
Fred C. Adams: The Degree of Fine-Tuning in our Universe – and Others 11 Feb 2019
Within our universe, the laws of physics have the proper form to support all of the building blocks that are needed for observers to arise. However, a large and growing body of research has argued that relatively small changes in the laws of physics could render the universe incapable of supporting life. In other words, the universe could be fine-tuned for the development of complexity. The list of required structures to have a life-permitting universe includes complex nuclei, planets, stars, galaxies, and the universe itself. In addition to their existence, these structures must have the right properties to support observers. Stable nuclei must populate an adequate fraction of the periodic table. Stars must be sufficiently hot and live for a long time. The galaxies must have gravitational potential wells that are deep enough to retain heavy elements produced by stars and not overly dense so that planets can remain in orbit. The universe itself must allow galaxies to form and live long enough for complexity to arise.
In order to make a full assessment of the degree of fine-tuning of the universe, one must address the following components of the problem:
I Specification of the relevant parameters of physics and astrophysics that can vary.
II Determination of the allowed ranges of parameters that allow for the development of complexity and hence observers.
III Identification of the underlying probability distributions from which the fundamental parameters are drawn, including the full possible range that the parameters can take.
IV Consideration of selection effects that allow the interpretation of observed properties in the context of the a priori probability distributions.
V Synthesis of the preceding ingredients to determine the overall likelihood for universes to become habitable
Studying the degree of tuning necessary for the universe to operate provides us with a greater understanding of how it works.
Both the fundamental constants that describe the laws of physics and the cosmological parameters that determine the properties of our universe must fall within a range of values in order for the cosmos to develop astrophysical structures and ultimately support life. 1 y. The standard model of particle physics contains both coupling constants a and particle masses.
The cosmological parameters, including
- the total energy density of the universe (Ω),
- the contribution from vacuum energy (ρΛ),
- the baryon-to-photon ratio (η),
- the dark matter contribution (δ),
- the amplitude of primordial density fluctuations (Q).
are quantities that are constrained by the requirements that the universe lives for a sufficiently long time emerges from the epoch of Big Bang Nucleosynthesis with an acceptable chemical composition, and can successfully produce large-scale structures such as galaxies. On smaller scales, stars and planets must be able to form and function. The stars must be sufficiently long-lived, have high enough surface temperatures, and have smaller masses than their host galaxies. The planets must be massive enough to hold onto an atmosphere, yet small enough to remain non-degenerate, and contain enough particles to support a biosphere of sufficient complexity. These requirements place constraints on
- the gravitational structure constant (αG),
- the fine structure constant (α),
- composite parameters (C?)
that specify nuclear reaction rates. Specific instances also require the fine-tuning in stellar nucleosynthesis, including the triple-alpha reaction that produces carbon. A fundamental question thus arises: What versions of the laws of physics are necessary for the development of astrophysical structures, which are in turn necessary for the development of life?
Physical Constants The progress of physics has revealed a host of physical constants, all of which have been measured to varying degrees of precision – for example, the speed of light (c), Planck’s constant (h¯), the gravitational constant (G), the charge of the electron (e), and the masses of various elementary particles like the proton (mp) and the electron (me). As physics has become progressively unified, the number of fundamental constants has reduced, but there is still a large number of them. The Standard Model of Particle Physics has 26, and the Standard Model of Cosmology has six constants.

It is well known that the Standard Model of Particle Physics has at least 26 parameters, but the theory must be extended to account for additional physics, including gravity, neutrino oscillations, dark matter, and dark energy
Cosmological Parameters and the Cosmic Inventory
A set of cosmological parameters are necessary to specify the current state of our universe. The current state of the universe can be characterized by a relatively small collection of parameters. The expansion of the universe is governed by the Friedmann equation. If we are concerned only with the expansion and evolution of the universe as a whole — and not the formation of structure within it — then the current state of the universe can be specified by measuring all of the contributions to the energy density ρ and the Hubble constant.

Table of the observed cosmological parameters in our universe.
These quantities have been measured by a number of cosmological experiments. The values are listed with few enough significant digits that they are consistent with all current measurements.
For our universe, the full range of allowed energy/time/mass scales spans a factor of ∼ 10^61. Similarly, the range of mass and size scales allowed by physical considerations span about 80^15. . If the parameter probabilities were distributed evenly in logarithmic space across a comparable range (of order 100 decades — see also the discussion below), then the allowed ranges of parameter space correspond to a few percent (maybe ∼ 1 − 10%) of the total. In contrast, if the parameters were distributed uniformly over the full range — and the viable parameters do not lie at the upper end of that range — then the allowed range would represent an incredibly small fraction of the total.
Although they represent a significant problem for particle physics theories, the observed hierarchies of the fundamental parameters are a distinguishing feature of the cosmos, and extreme hierarchies are required for any universe to be viable: The strength of gravity can vary over several orders of magnitude, but it must remain weak compared to other forces so that the universe can evolve and produce structure, and stars can function. This required weakness of gravity leads to the hierarchies of scale that we observe in the universe. In addition, any working universe requires a clean separation of the energies corresponding to the vacuum, atoms, nuclei, electroweak symmetry breaking, and the Planck scale. In other words, the hierarchies of physics lead to the observed hierarchies of astrophysics, and this ordering is necessary for a habitable universe. The universe is surprisingly resilient to changes in its fundamental and cosmological parameters.
Robin Collins: The Argument from Physical Constants: The Fine-Tuning for Discoverability 3
The Higgs boson is a key particle of our most fundamental model of particle physics, called the Standard Model (SM). The SM is the most fundamental physical model regarding the ultimate structure of matter. It is generally thought to be incomplete, a low-energy approximation to a deeper theory; in the forty years since its existence, however, it has withstood every test. It consists of a set of elementary particles and laws governing their interactions. These particles are the quarks and leptons; the particles that carry the electromagnetic, weak, and strong forces (called the gauge bosons); and the recently discovered Higgs boson. Quarks and leptons come in generations. The particles in a given row are identical except for their mass, with the mass of the particles increases with each generation: for example, the charm quark is about 500 times more massive than the up quark, and the top quark is about 130 times as massive as the charm quark. Only the first generation plays a direct role in life. Specifically, atoms are composed of electrons orbiting a nucleus composed of protons and neutrons, with the protons being composed of two up quarks and one down quark, and the neutron is composed of two down quarks and one up quark. Even though protons and neutrons are made of quarks, most of their mass does not come from the quarks but from the strong force that binds the quarks together.
Casey Luskin: The Fine-Tuning of the Universe November 8, 2017 2
The following gives a sense of the degree of fine-tuning that must go into some of these values to yield a life-friendly universe:
Gravitational constant: 1 part in 10^34
Electromagnetic force versus force of gravity: 1 part in 10^37
Cosmological constant: 1 part in 10^120
Mass density of universe: 1 part in 10^59
Expansion rate of universe: 1 part in 10^55
Initial entropy: 1 part in 10^ (10^123)
The last item in the list — the initial entropy of the universe — shows an astounding degree of fine-tuning.
Paul Davies's book The Goldilocks Enigma (2006) reviews the current state of the fine tuning debate in detail, and concludes by enumerating the following responses to that debate:
The absurd universe: Our universe just happens to be the way it is.
The unique universe: There is a deep underlying unity in physics that necessitates the Universe being the way it is. Some Theory of Everything will explain why the various features of the Universe must have exactly the values that we see.
The multiverse: Multiple universes exist, having all possible combinations of characteristics, and we inevitably find ourselves within a universe that allows us to exist.
Intelligent design: A creator designed the Universe with the purpose of supporting complexity and the emergence of intelligence.
The life principle: There is an underlying principle that constrains the Universe to evolve towards life and mind.
The self-explaining universe: A closed explanatory or causal loop: "perhaps only universes with a capacity for consciousness can exist". This is Wheeler's Participatory Anthropic Principle (PAP).
The fake universe: We live inside a virtual reality simulation.
a: In physics, a coupling constant or gauge coupling parameter (or, more simply, a coupling), is a number that determines the strength of the force exerted in an interaction.
1. https://arxiv.org/pdf/1902.03928.pdf
2. https://evolutionnews.org/2017/11/ids-top-six-the-fine-tuning-of-the-universe/
3. http://library.lol/main/643DEBF15D83B06F4AD0F574F37883FA
4. https://arxiv.org/pdf/2012.05617.pdf

Last edited by Otangelo on Fri Apr 29, 2022 4:50 am; edited 15 times in total