Global Optimization, Local Adaptation, and the Role of Growth in Distribution Networks 1
https://reasonandscience.catsboard.com/t2451-global-optimization-local-adaptation-and-the-role-of-growth-in-distribution-networks
Highly-optimized complex transport networks serve crucial functions in many man-made and natural systems such as power grids and plant or animal vasculature. Often, the relevant optimization functional is non-convex and characterized by many local extrema. In general, finding the global, or nearly global optimum is difficult. In biological systems, it is believed that such an optimal state is slowly achieved through natural selection. However, general coarse-grained models for flow networks with local positive feedback rules for the vessel conductivity typically get trapped in low efficiency, local minima. In this work, we show how the growth of the underlying tissue, coupled to the dynamical equations for network development, can drive the system to a dramatically improved optimal state. This general model provides a surprisingly simple explanation for the appearance of highly optimized transport networks in biology such as leaf and animal vasculature.
Complex life requires distribution networks: veins and arteries in animals, xylem and phloem in plants, and even fungal mycelia that deliver nutrients and collect the byproducts of metabolism. The efficient function of these distribution networks is crucial for an organism’s fitness. Thus, biological transport networks are thought to have undergone a process of gradual optimization through evolution, culminating in organizational principles such
as Murray’s law. A particular class of such networks that minimizes flow resistance under biologically relevant constraints has been studied to reveal a wealth of phenomena such as phase transitions, the interdependence
of flow and conduit geometry, and predictions about allometric scaling relations in biology. When the optimization models are generalized to require resilience to damage or to consider fluctuations in the load, optimal networks reproduce the reticulate network patterns observed in biological systems. The optimality principles that often determine these networks also appear in non-biological context, e.g., river basins and are relevant for man-made systems such as gas or sewage pipe networks
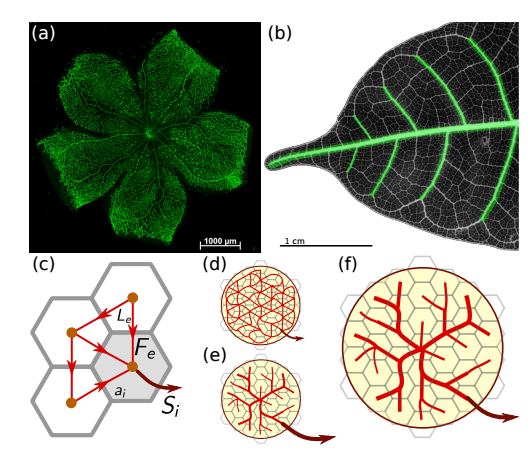
FIG. 1.
(a) Immunostained mouse pup retina 7 days after birth. The hierarchical vascular network is clearly visible.
b) Chemically cleared and stained leaf of Protium wanningianum. The first two levels of vascular hierarchy are marked in green.
(c) Network representation of vascular flow. Edges (red, with lengths Le) carry flows Fe (arrows). At nodes (orange, representing areas ai), net currents Si (dark red arrows, only one shown for clarity) are drawn from the network, supplying the surrounding tissue.
(d-f) Sketch of vascular development. Overlaid in grey is a co-moving coarse-graining grid. At the beginning
(d), a tightly meshed capillary plexus is formed (capillaries in red). During development, the plexus is pruned and a hierarchical vascular tree is formed either due to
(e) increasing perfusion, or
(f) growth.
a simple physical mechanism such as growth may have been selected for over the course of evolution to produce highly optimized venation in plants and animals. Growth effectively reduces the dimension of the evolutionary search space to two parameters that can be used to explore the energy landscape. Studying appropriate mutants in plants (e.g., similar to) or animals could verify our model. Finally, we suggest that similar biologically-inspired dynamics could help improve solutions to other global optimization problems.
1. https://arxiv.org/pdf/1606.00331.pdf
https://reasonandscience.catsboard.com/t2451-global-optimization-local-adaptation-and-the-role-of-growth-in-distribution-networks
Highly-optimized complex transport networks serve crucial functions in many man-made and natural systems such as power grids and plant or animal vasculature. Often, the relevant optimization functional is non-convex and characterized by many local extrema. In general, finding the global, or nearly global optimum is difficult. In biological systems, it is believed that such an optimal state is slowly achieved through natural selection. However, general coarse-grained models for flow networks with local positive feedback rules for the vessel conductivity typically get trapped in low efficiency, local minima. In this work, we show how the growth of the underlying tissue, coupled to the dynamical equations for network development, can drive the system to a dramatically improved optimal state. This general model provides a surprisingly simple explanation for the appearance of highly optimized transport networks in biology such as leaf and animal vasculature.
Complex life requires distribution networks: veins and arteries in animals, xylem and phloem in plants, and even fungal mycelia that deliver nutrients and collect the byproducts of metabolism. The efficient function of these distribution networks is crucial for an organism’s fitness. Thus, biological transport networks are thought to have undergone a process of gradual optimization through evolution, culminating in organizational principles such
as Murray’s law. A particular class of such networks that minimizes flow resistance under biologically relevant constraints has been studied to reveal a wealth of phenomena such as phase transitions, the interdependence
of flow and conduit geometry, and predictions about allometric scaling relations in biology. When the optimization models are generalized to require resilience to damage or to consider fluctuations in the load, optimal networks reproduce the reticulate network patterns observed in biological systems. The optimality principles that often determine these networks also appear in non-biological context, e.g., river basins and are relevant for man-made systems such as gas or sewage pipe networks

FIG. 1.
(a) Immunostained mouse pup retina 7 days after birth. The hierarchical vascular network is clearly visible.
b) Chemically cleared and stained leaf of Protium wanningianum. The first two levels of vascular hierarchy are marked in green.
(c) Network representation of vascular flow. Edges (red, with lengths Le) carry flows Fe (arrows). At nodes (orange, representing areas ai), net currents Si (dark red arrows, only one shown for clarity) are drawn from the network, supplying the surrounding tissue.
(d-f) Sketch of vascular development. Overlaid in grey is a co-moving coarse-graining grid. At the beginning
(d), a tightly meshed capillary plexus is formed (capillaries in red). During development, the plexus is pruned and a hierarchical vascular tree is formed either due to
(e) increasing perfusion, or
(f) growth.
a simple physical mechanism such as growth may have been selected for over the course of evolution to produce highly optimized venation in plants and animals. Growth effectively reduces the dimension of the evolutionary search space to two parameters that can be used to explore the energy landscape. Studying appropriate mutants in plants (e.g., similar to) or animals could verify our model. Finally, we suggest that similar biologically-inspired dynamics could help improve solutions to other global optimization problems.
1. https://arxiv.org/pdf/1606.00331.pdf


