https://reasonandscience.catsboard.com/t1336-laws-of-physics-fine-tuned-for-a-life-permitting-universe
The laws of physics aren't a "free lunch", that just exists, and that does not require an explanation. If the fundamental constants had substantially different values, it would be impossible to form even simple structures like atoms, molecules, planets, or stars. Paul Davies,The Goldilocks enigma: For a start, there is no logical reason why nature should have a mathematical subtext in the first place. You would never guess by looking at the physical world that beneath the surface hubbub of natural phenomena lies an abstract order, an order that cannot be seen or heard or felt, but only deduced.
The existence of laws of nature is the starting point of science itself. But right at the outset we encounter an obvious and profound enigma: Where do the laws of nature come from? If they aren’t the product of divine providence, how can they be explained? English astronomer James Jeans: “The universe appears to have been designed by a pure mathematician.”
Sir Fred Hoyle: I do not believe that any scientist who examines the evidence would fail to draw the inference that the laws of nuclear physics have been deliberately designed with regard to the consequences they produce inside stars. If this is so, then my apparently random quirks have become part of a deep-laid scheme. If not then we are back again at a monstrous sequence of accidents.
How could the whole world of nature have ever precisely obeyed laws that did not yet exist? But where did they exist? A law is simply an idea, and an idea exists only in someone's mind. Since there is no mind in nature, nature itself has no intelligence of the laws which govern it. Modern science takes it for granted that the universe has always danced to rhythms it cannot hear, but still assigns power of motion to the dancers themselves. How is that possible? The power to make things happen in obedience to universal laws cannot reside in anything ignorant of these laws. Would it be more reasonable to suppose that this power resides in the laws themselves? Of course not. Ideas have no intrinsic power. They affect events only as they direct the will of a thinking person. Only a thinking person has the power to make things happen. Since natural events were lawful before man ever conceived of natural laws, the thinking person responsible for the orderly operation of the universe must be a higher Being, a Being we know as God.
Roger Penrose
The Second Law of thermodynamics is one of the most fundamental principles of physics
https://accelconf.web.cern.ch/e06/papers/thespa01.pdf
Ethan Siegel What Is The Fine Structure Constant And Why Does It Matter? May 25, 2019,
Why is our Universe the way it is, and not some other way? There are only three things that make it so: the laws of nature themselves, the fundamental constants governing reality, and the initial conditions our Universe was born with. If the fundamental constants had substantially different values, it would be impossible to form even simple structures like atoms, molecules, planets, or stars. Yet, in our Universe, the constants have the explicit values they do, and that specific combination yields the life-friendly cosmos we inhabit.
https://www.forbes.com/sites/forbes-personal-shopper/2021/08/12/artifact-uprising-early-years-child-memory-book/?sh=3576094116ca
Jason Waller Cosmological Fine-Tuning Arguments 2020, page 107
Fine-Tuning and Metaphysics
There may also be a number of ways in which our universe is “meta-physically” fine-tuned. Let’s consider three examples: the law-like nature of our universe, the psychophysical laws, and emergent properties. The first surprising metaphysical fact about our universe is that it obeys laws. It is not difficult to coherently describe worlds that are entirely chaotic and have no laws at all. There are an infinite number of such possible worlds. In such worlds, of course, there could be no life because there would be no stability and so no development. Furthermore, we can imagine a universe in which the laws of nature change rapidly every second or so. It is hard to calculate precisely what would happen here (of course), but without stable laws of nature it is hard to imagine how intelligent organic life could evolve. If, for example, opposite electrical charges began to repulse one another from time to time, then atoms would be totally unstable. Similarly, if the effect that matter had on the geometry of space-time changed hourly, then we could plausibly infer that such a world would lack the required consistency for life to flourish. Is it possible to quantify this metaphysical fine-tuning more precisely? Perhaps. Consider the following possibility. ( If we hold to the claim that the universe is 13,7bi years old ) - there have been approximately 10^18 seconds since the Big Bang. So far as we can tell the laws of nature have not changed in all of that time. Nevertheless, it is easy to come up with a huge number of alternative histories where the laws of nature changed radically at time t1 , or time t2 , etc. If we confine ourselves only to a single change and only allow one change per second, then we can easily develop 10^18 alternative metaphysical histories of the universe. Once we add other changes, we get an exponentially larger number. If (as seems very likely) most of those universes are not life-permitting, then we could have a significant case of metaphysical fine-tuning.
The existence of organic intelligent life relies on numerous emergent properties—liquidity, chemical properties, solidity, elasticity, etc. Since all of these properties are required for the emergence of organic life, if the supervenience laws had been different, then the same micro-level structures would have yielded different macro-level properties. That may very well have meant that no life could be posssible. If atoms packed tightly together did not result in solidity, then this would likely limit the amount of biological complexity that is possible. Michael Denton makes a similar argument concerning the importance of the emergent properties of water to the possibility of life. While these metaphysical examples are much less certain than the scientific ones, they are suggestive and hint at the many different ways in which our universe appears to have been fine-tuned for life.
https://3lib.net/book/5240658/bd3f0d
Steven Weinberg: The laws of nature are the principles that govern everything. The aim of physics, or at least one branch of physics, is after all to find the principles that explain the principles that explain everything we see in nature, to find the ultimate rational basis of the universe. And that gets fairly close in some respects to what people have associated with the word "God. The outside world is governed by mathematical laws. We can look forward to a theory that encompasses all existing theories, which unifies all the forces, all the particles, and at least in principle is capable of serving as the basis of an explanation of everything. We can look forward to that, but then the question will always arise, "Well, what explains that? Where does that come from?" And then we -- looking at -- standing at that brink of that abyss we have to say we don't know, and how could we ever know, and how can we ever get comfortable with this sort of a world ruled by laws which just are what they are without any further explanation? And coming to that point which I think we will come to, some would say, well, then the explanation is God made it so. If by God you mean a personality who is concerned about human beings, who did all this out of love for human beings, who watches us and who intervenes, then I would have to say in the first place how do you know, what makes you think so?
https://www.pbs.org/faithandreason/transcript/wein-frame.html
My response: The mere fact that the universe is governed by mathematical laws, and that the fundamental physical constants are set just right to permit life, is evidence enough.
ROBIN COLLINS The Teleological Argument: An Exploration of the Fine-Tuning of the Universe 2009
The first major type of fine-tuning is that of the laws of nature. The laws and principles of nature themselves have just the right form to allow for the existence of embodied moral agents. To illustrate this, we shall consider the following five laws or principles (or causal powers) and show that if any one of them did not exist, self-reproducing, highly complex material systems could not exist:
(1) a universal attractive force, such as gravity;
(2) a force relevantly similar to that of the strong nuclear force, which binds protons and neutrons together in the nucleus;
(3) a force relevantly similar to that of the electromagnetic force;
(4) Bohr’s Quantization Rule or something similar;
(5) the Pauli Exclusion Principle. If any one of these laws or principles did not exist (and were not replaced by a law or principle that served the same or similar role), complex self-reproducing material systems could not evolve.
First, consider gravity. Gravity is a long-range attractive force between all material objects, whose strength increases in proportion to the masses of the objects and falls off with the inverse square of the distance between them. Consider what would happen if there were no universal, long-range attractive force between material objects, but all the other fundamental laws remained (as much as possible) the same. If no such force existed, then there would be no stars, since the force of gravity is what holds the matter in stars together against the outward forces caused by the high internal temperatures inside the stars. This means that there would be no long-term energy sources to sustain the evolution (or even existence) of highly complex life. Moreover, there probably would be no planets, since there would be nothing to bring material particles together, and even if there were planets (say because planet-sized objects always existed in the universe and were held together by cohesion), any beings of significant size could not move around without floating off the planet with no way of returning. This means that physical life could not exist. For all these reasons, a universal attractive force such as gravity is required for life.
Question: Why is gravity only attractive, and not repulsive? It could be both, and there would be no life in the universe.
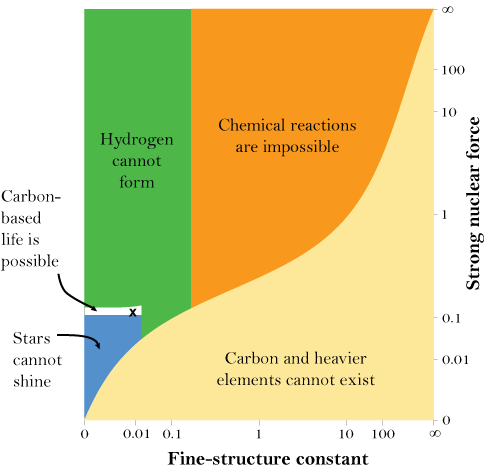
Second, consider the strong nuclear force. The strong nuclear force is the force that binds nucleons (i.e. protons and neutrons) together in the nucleus of an atom. Without it, the nucleons would not stay together. It is actually a result of a deeper force, the “gluonic force,” between the quark constituents of the neutrons and protons, a force described by the theory of quantum chromodynamics. It must be strong enough to overcome the repulsive electromagnetic force between the protons and the quantum zero-point energy of the nucleons. Because of this, it must be considerably stronger than the electromagnetic force; otherwise, the nucleus would come apart. Further, to keep atoms of limited size, it must be very short range – which means its strength must fall off much, much more rapidly than the inverse square law characteristic of the electromagnetic force and gravity. Since it is a purely attractive force (except at extraordinarily small distances), if it fell off by an inverse square law like gravity or electromagnetism, it would act just like gravity and pull all the protons and neutrons in the entire universe together. In fact, given its current strength, around 10^40 stronger than the force of gravity between the nucleons in a nucleus, the universe would most likely consist of a giant black hole. Thus, to have atoms with an atomic number greater than that of hydrogen, there must be a force that plays the same role as the strong nuclear force – that is, one that is much stronger than the electromagnetic force but only acts over a very short range. It should be clear that embodied moral agents could not be formed from mere hydrogen, contrary to what one might see on science fiction shows such as Star Trek. One cannot obtain enough self-reproducing, stable complexity. Furthermore, in a universe in which no other atoms but hydrogen could exist, stars could not be powered by nuclear fusion, but only by gravitational collapse, thereby drastically decreasing the time for, and hence the probability of, the evolution of embodied life.
Questions: Why is the strong force not both, repulsive and attractive? It could be both, and we would not be here to talk about it.
Third, consider electromagnetism. Without electromagnetism, there would be no atoms, since there would be nothing to hold the electrons in orbit. Further, there would be no means of transmission of energy from stars for the existence of life on planets. It is doubtful whether enough stable complexity could arise in such a universe for even the simplest forms of life to exist.
Fourth, consider Bohr’s rule of quantization, first proposed in 1913, which requires that electrons occupy only fixed orbitals (energy levels) in atoms. It was only with the development of quantum mechanics in the 1920s and 1930s that Bohr’s proposal was given an adequate theoretical foundation. If we view the atom from the perspective of classical Newtonian mechanics, an electron should be able to go in any orbit around the nucleus. The reason is the same as why planets in the solar system can be any distance from the Sun – for example, the Earth could have been 150 million miles from the Sun instead of its present 93 million miles. Now the laws of electromagnetism – that is, Maxwell’s equations – require that any charged particle that is accelerating emit radiation. Consequently, because electrons orbiting the nucleus are accelerating – since their direction of motion is changing – they would emit radiation. This emission would in turn cause the electrons to lose energy, causing their orbits to decay so rapidly that atoms could not exist for more than a few moments. This was a major problem confronting Rutherford’s model of the atom – in which the atom had a nucleus with electrons around the nucleus – until Niels Bohr proposed his ad hoc rule of quantization in 1913, which required that electrons occupy fixed orbitals. Thus, without the existence of this rule of quantization – or something relevantly similar – atoms could not exist, and hence there would be no life.
Finally, consider the Pauli Exclusion Principle, which dictates that no two fermions (spin-½ particles) can occupy the same quantum state. This arises from a deep principle in quantum mechanics which requires that the joint wave function of a system of fermions be antisymmetric. This implies that not more than two electrons can occupy the same orbital in an atom, since a single orbital consists of two possible quantum states (or more precisely, eigenstates) corresponding to the spin pointing in one direction and the spin pointing in the opposite direction. This allows for complex chemistry since without this principle, all electrons would occupy the lowest atomic orbital. Thus, without this principle, no complex life would be possible.
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.696.63&rep=rep1&type=pdf
Alexander Bolonkin Universe, Human Immortality and Future Human Evaluation, 2012
There is no explanation for the particular values that physical constants appear to have throughout our universe, such as Planck’s constant h or the gravitational constant G. Several conservation laws have been identified, such as the conservation of charge, momentum, angular momentum, and energy; in many cases, these conservation laws can be related to symmetries or mathematical identities.
https://3lib.net/book/2205001/d7ffa2
On the last page of his book Many Worlds in One, Alex Vilenkin says this:
“The picture of quantum tunneling from nothing raises another intriguing question. The tunneling process is governed by the same fundamental laws that describe the subsequent evolution of the universe. It follows that the laws should be “there” even prior to the universe itself. Does this mean that the laws are not mere descriptions of reality and can have an independent existence of their own? In the absence of space, time, and matter, what tablets could they be written upon? The laws are expressed in the form of mathematical equations. If the medium of mathematics is the mind, does this mean that mind should predate the universe?”
Vilenkin, Alex. Many Worlds in One: The Search for Other Universes (pp. 204-206). Farrar, Straus and Giroux.
Luke A. Barnes The Fine-Tuning of the Universe for Intelligent Life June 11, 2012
Changing the Laws of Nature
The set of laws that permit the emergence and persistence of complexity is a very small subset of all possible laws. There is an infinite number of ways to set up laws that would result in an either trivially simple or utterly chaotic universe.
- A universe governed by Maxwell’s Laws “all the way down” (i.e. with no quantum regime at small scales) will not have stable atoms — electrons radiate their kinetic energy and spiral rapidly into the nucleus — and hence no chemistry. We don’t need to know what the parameters are to know that life in such a universe is plausibly impossible.
- If electrons were bosons, rather than fermions, then they would not obey the Pauli exclusion principle. There would be no chemistry.
- If gravity were repulsive rather than attractive, then matter wouldn’t clump into complex structures. Remember: your density, thank gravity, is 10^30 times greater than the average density of the universe.
- If the strong force were a long rather than short-range force, then there would be no atoms. Any structures that formed would be uniform, spherical, undifferentiated lumps, of arbitrary size and incapable of complexity.
- If, in electromagnetism, like charges attracted and opposites repelled, then there would be no atoms. As above, we would just have undifferentiated lumps of matter.
- The electromagnetic force allows matter to cool into galaxies, stars, and planets. Without such interactions, all matter would be like dark matter, which can only form into large, diffuse, roughly spherical haloes of matter whose only internal structure consists of smaller, diffuse, roughly spherical subhaloes.
https://arxiv.org/pdf/1112.4647.pdf
Leonard Susskind The Cosmic Landscape: String Theory and the Illusion of Intelligent Design 2006, page 100
The Laws of Physics are like the “weather of the vacuum,” except instead of the temperature, pressure, and humidity, the weather is determined by the values of fields. And just as the weather determines the kinds of droplets that can exist, the vacuum environment determines the list of elementary particles and their properties. How many controlling fields are there, and how do they affect the list of elementary particles, their masses, and coupling constants? Some of the fields we already know—the electric field, the magnetic field, and the Higgs field. The rest will be known only when we discover more about the overarching laws of nature than just the Standard Model.
https://3lib.net/book/2472017/1d5be1
By law in physics, or physical laws of nature, what one means is that the physical forces that govern the universe remain constant - they do not change across the universe. One relevant question, Lawrence Krauss asks, is: If we change one fundamental constant, one force law, would the whole edifice tumble? 5 There HAVE to be four forces in nature, the proton requires to be 1836 times heavier than the electron, etc, otherwise, the universe would be devoid of life.
String theorists argued that they had found the Theory of Everything—that using the postulates of string theory one would be driven to a unique physical theory, with no wiggle room, that would ultimately explain everything we see at a fundamental level.
My comment: The Theory of everything is basically synonymous with a mechanism, that without external guidance or set-up, would explain how the universe got set up like a clock, operating in a continuous stable manner, and permitting the generation of the right initial condition to have a continuously expanding universe, atoms, the periodic table containing all the chemical elements, stars, planets, molecules, life, and humans with brains, being able to investigate all this. Basically, it would replace God.
WH. McCrea: "Cosmology after Half a Century," Science, Vol. 160, June 1968, p. 1297.
"The naive view implies that the universe suddenly came into existence and found a complete system of physical laws waiting to be obeyed. Actually, it seems more natural to suppose that the physical universe and the laws of physics are interdependent." —
https://sci-hub.ren/10.1126/science.160.3834.1295
My comment: The laws of physics are interdependent with time, space, and matter. They exist to govern matter within our linear dimension of time and space. Because the laws of physics are interdependent with all forms of matter, they must therefore have existed simultaneously with matter in our universe. Time, space, and matter we’re created at the very moment of “the beginning”, and as such, so did the laws of physics.
Paul Davies: Superforce, page 243
All the evidence so far indicates that many complex structures depend most delicately on the existing form of these laws. It is tempting to believe, therefore, that a complex universe will emerge only if the laws of physics are very close to what they are....The laws, which enable the universe to come into being spontaneously, seem themselves to be the product of exceedingly ingenious design. If physics is the product of design, the universe must have a purpose, and the evidence of modern physics suggests strongly to me that the purpose includes us.
https://3lib.net/book/14357613/6ebdf9
Paul Davies,The Goldilocks enigma: why is the universe just right for life? 2006
Until recently, “the Goldilocks factor” was almost completely ignored by scientists. Now, that is changing fast. Science is, at last, coming to grips with the enigma of why, at last, verse is so uncannily fit for life. The explanation entails understanding how the universe began and evolved into its present form and knowing what matter is made of and how it is shaped and structured by the different forces of nature. Above all, it requires us to probe the very nature of physical laws. The existence of laws of nature is the starting point of science itself. But right at the outset we encounter an obvious and profound enigma: Where do the laws of nature come from? As I have remarked, Galileo, Newton, and their contemporaries regarded the laws as thoughts in the mind of God, and their elegant mathematical form as a manifestation of God’s rational plan for the universe. Few scientists today would describe the laws of nature using such quaint language. Yet the questions remain of what these laws are and why they have the form that they do. If they aren’t the product of divine providence, how can they be explained?
English astronomer James Jeans: “The universe appears to have been designed by a pure mathematician.”
https://3lib.net/book/5903498/82353b
Paul Davies Yes, the universe looks like a fix. But that doesn't mean that a god fixed it 26 Jun 2007
The idea of absolute, universal, perfect, immutable laws comes straight out of monotheism, which was the dominant influence in Europe at the time science as we know it was being formulated by Isaac Newton and his contemporaries. Just as classical Christianity presents God as upholding the natural order from beyond the universe, so physicists envisage their laws as inhabiting an abstract transcendent realm of perfect mathematical relationships. Furthermore, Christians believe the world depends utterly on God for its existence, while the converse is not the case. Correspondingly, physicists declare that the universe is governed by eternal laws, but the laws remain impervious to events in the universe. I propose instead that the laws are more like computer software: programs being run on the great cosmic computer. They emerge with the universe at the big bang and are inherent in it, not stamped on it from without like a maker's mark. If a law is a truly exact mathematical relationship, it requires infinite information to specify it. In my opinion, however, no law can apply to a level of precision finer than all the information in the universe can express. Infinitely precise laws are an extreme idealisation with no shred of real world justification. In the first split second of cosmic existence, the laws must therefore have been seriously fuzzy. Then, as the information content of the universe climbed, the laws focused and homed in on the life-encouraging form we observe today. But the flaws in the laws left enough wiggle room for the universe to engineer its own bio-friendliness. Thus, three centuries after Newton, symmetry is restored: the laws explain the universe even as the universe explains the laws. If there is an ultimate meaning to existence, as I believe is the case, the answer is to be found within nature, not beyond it. The universe might indeed be a fix, but if so, it has fixed itself.
https://www.theguardian.com/commentisfree/2007/jun/26/spaceexploration.comment
My comment: Thats similar to say that the universe created itself. Thats simply irrational philosophical gobbledygook. The laws of physics had to be imprinted from an outside source right at the beginning. Any fiddling around until finding the right parameters to have the right conditions for an expanding universe would have taken trillions and trillions of attempts. If not God, nature must have had an urgent need to become self-existent. Why or how would that have been so?
Sir Fred Hoyle: [Fred Hoyle, in Religion and the Scientists, 1959; quoted in Barrow and Tipler, p. 22]
I do not believe that any scientist who examines the evidence would fail to draw the inference that the laws of nuclear physics have been deliberately designed with regard to the consequences they produce inside stars. If this is so, then my apparently random quirks have become part of a deep-laid scheme. If not then we are back again at a monstrous sequence of accidents.
Finally, it would be the ultimate anthropic coincidence if beauty and complexity in the mathematical principles of the fundamental theory of physics produced all the necessary lowenergy conditions for intelligent life. This point has been made by a number of authors, e.g. Carr & Rees (1979) and Aguirre (2005). Here is
Wilczek (2006b): “It is logically possible that parameters determined uniquely by abstract theoretical principles just happen to exhibit all the apparent fine-tunings required to produce, by a lucky coincidence, a universe containing complex structures. But that, I think, really strains credulity.”
https://arxiv.org/pdf/1112.4647.pdf
Luke A. Barnes: A Reasonable Little Question: A Formulation of the Fine-Tuning Argument No. 42, 2019–2020 1
The standard model of particle physics and the standard model of cosmology (together, the standard models) contain 31 fundamental constants (which, for our purposes here, will include what are better known as initial conditions or boundary conditions) listed in Tegmark, Aguirre, Rees, and Wilczek (2006):
2 constants for the Higgs field: the vacuum expectation value (vev) and the Higgs mass,
12 fundamental particle masses, relative to the Higgs vev (i.e., the Yukawa couplings): 6 quarks (u,d,s,c,t,b) and 6 leptons (e,μ, τ, νe, νμ, ντ)
3 force coupling constants for the electromagnetic (α), weak (αw) and strong (αs) forces,
4 parameters that determine the Cabibbo-Kobayashi-Maskawa matrix, which describes the mixing of quark flavours by the weak force,
4 parameters of the Pontecorvo-Maki-Nakagawa-Sakata matrix, which describe neutrino mixing,
1 effective cosmological constant (Λ),
3 baryon (i.e., ordinary matter) / dark matter / neutrino mass per photon ratios,
1 scalar fluctuation amplitude (Q),
1 dimensionless spatial curvature (κ≲10−60).
This does not include 4 constants that are used to set a system of units of mass, time, distance and temperature: Newton’s gravitational constant (G), the speed of light c, Planck’s constant ℏ, and Boltzmann’s constant kB. There are 25 constants from particle physics, and 6 from cosmology.
About ten to twelve out of these above-mentioned constants, thirty-one total, exhibit significant fine-tuning.
https://quod.lib.umich.edu/e/ergo/12405314.0006.042/--reasonable-little-question-a-formulation-of-the-fine-tuning?rgn=main;view=fulltext
Max Tegmark et al.: Dimensionless constants, cosmology, and other dark matters 2006

The origin of the dimensionless numbers
So why do we observe these 31 parameters to have the particular values listed in Table I? Interest in that question has grown with the gradual realization that some of these parameters appear fine-tuned for life, in the sense that small relative changes to their values would result in dramatic qualitative changes that could preclude intelligent life, and hence the very possibility of reflective observation. There are four common responses to this realization:
(1) Fluke—Any apparent fine-tuning is a fluke and is best ignored
(2) Multiverse—These parameters vary across an ensemble of physically realized and (for all practical purposes) parallel universes, and we find ourselves in one where life is possible.
(3) Design—Our universe is somehow created or simulated with parameters chosen to allow life.
(4) Fecundity—There is no fine-tuning because intelligent life of some form will emerge under extremely varied circumstances.
Options 1, 2, and 4 tend to be preferred by physicists, with recent developments in inflation and high-energy theory giving new popularity to option 2.
https://sci-hub.ren/10.1103/physrevd.73.023505
My comment: This is an interesting confession. Pointing to option 2, a multiverse, is based simply on personal preference, but not on evidence.
Michio Kaku on The God Equation | Closer To Truth Chats
There are four forces that govern the entire universe we find no exceptions to gravity which holds us onto the floor keeps the sun from exploding we have the electromagnetic force that lights up our cities
then we have the two nuclear forces the weak and the strong forces and we want a theory of all four forces remember that all of biology can be explained by chemistry all of chemistry can be explained by physics all of physics can be explained by two great theories relativity the theory of gravity and the quantum theory which summarizes the electromagnetic force and the two nuclear forces but to bring them together that would give us a theory of
everything all known physical phenomenon can be summarized by an equation perhaps no more than one inch long that will allow us to quote read the mind of god and these are the words of albert einstein who spent the last 30 years of his life chasing after this theory of everything the god equation. String theory is the only theory that can unify all four of the fundamental forces including gravitational corrections
https://www.youtube.com/watch?v=B9N2S6Chz44
Stephen C. Meyer: The return of the God hypothesis, page 189
Consider that several key fine-tuning parameters—in particular, the values of the constants of the fundamental laws of physics— are intrinsic to the structure of those laws. In other words, the precise “dial settings” of the different constants of physics represent specific features of the laws of physics themselves—just how strong gravitational attraction or electromagnetic attraction will be, for example. These specific and contingent values cannot be explained by the laws of physics because they are part of the logical structure of those laws. Scientists who say otherwise are just saying that the laws of physics explain themselves. But that is reasoning in a circle.
pg.569: In addition to the values of constants within the laws of physics, the fundamental laws themselves have specific mathematical and logical structures that could have been otherwise—that is, the laws themselves have contingent rather than logically necessary features. Yet the existence of life in the universe depends on the fundamental laws of nature having the precise mathematical structures that they do. For example, both Newton’s universal law of gravitation and Coulomb’s law of electrostatic attraction describe forces that diminish with the square of the distance. Nevertheless, without violating any logical principle or more fundamental law of physics, these forces could have diminished with the cube (or higher exponent) of the distance. That would have made the forces they describe too weak to allow for the possibility of life in the universe. Conversely, these forces might just as well have diminished in a strictly linear way. That would have made them too strong to allow for life in the universe. Moreover, life depends upon the existence of various different kinds of forces—which we describe with different kinds of laws— acting in concert. For example, life in the universe requires:
(1) a long-range attractive force (such as gravity) that can cause galaxies, stars, and planetary systems to congeal from chemical elements in order to provide stable platforms for life;
(2) a force such as the electromagnetic force to make possible chemical reactions and energy transmission through a vacuum;
(3) a force such as the strong nuclear force operating at short distances to bind the nuclei of atoms together and overcome repulsive electrostatic forces;
(4) the quantization of energy to make possible the formation of stable atoms and thus life;
(5) the operation of a principle in the physical world such as the Pauli exclusion principle that (a) enables complex material structures to form and yet (b) limits the atomic weight of elements (by limiting the number of neutrons in the lowest nuclear shell). Thus, the forces at work in the universe itself (and the mathematical laws of physics describing them) display a fine-tuning that requires explanation. Yet, clearly, no physical explanation of this structure is possible, because it is precisely physics (and its most fundamental laws) that manifests this structure and requires explanation. Indeed, clearly physics does not explain itself. See Gordon, “Divine Action and the World of Science,” esp. 258–59; Collins, “The Fine-Tuning Evidence Is Convincing,” esp. 36–38.
https://3lib.net/book/15644088/9c418b
Paul Davies: The Goldilocks Enigma: Why Is the Universe Just Right for Life? 2008
The universe obeys mathematical laws; they are like a hidden subtext in nature. Science reveals that there is a coherent scheme of things, but scientists do not necessarily interpret that as evidence for meaning or purpose in the universe.
My comment: The only rational explanation is however that God created this coherent scheme of things since there is no other alternative explanation. That's why atheists rather than admit that, prefer to argue of " not knowing " of its cause
This cosmic order is underpinned by definite mathematical laws that interweave each other to form a subtle and harmonious unity. The laws are possessed of an elegant simplicity, and have often commended themselves to scientists on grounds of beauty alone. Yet these same simple laws permit matter and energy to self-organize into an enormous variety of complex states. If the universe is a manifestation of rational order, then we might be able to deduce the nature of the world from "pure thought" alone, without the need for observation or experiment. On the other hand, that same logical structure contains within itself its own paradoxical limitations that ensure we can never grasp the totality of existence from deduction alone.
Why should nature be governed by laws? Why should those laws be expressible in terms of mathematics?
The physical universe and the laws of physics are interdependent and irreducible. There would not be one without the other. Origins make only sense in face of Intelligent Design.
"The naive view implies that the universe suddenly came into existence and found a complete system of physical laws waiting to be obeyed. Actually, it seems more natural to suppose that the physical universe and the laws of physics are interdependent." —*WH. McCrea, "Cosmology after Half a Century," Science, Vol. 160, June 1968, p. 1297.
Our very ability to establish the laws of nature depends on their stability.(In fact, the idea of a law of nature implies stability.) Likewise, the laws of nature must remain constant long enough to provide the kind of stability life requires through the building of nested layers of complexity. The properties of the most fundamental units of complexity we know of, quarks, must remain constant in order for them to form larger units, protons and neutrons, which then go into building even larger units, atoms, and so on, all the way to stars, planets, and in some sense, people. The lower levels of complexity provide the structure and carry the information of life. There is still a great deal of mystery about how the various levels relate, but clearly, at each level, structures must remain stable over vast stretches of space and time.
And our universe does not merely contain complex structures; it also contains elaborately nested layers of higher and higher complexity. Consider complex carbon atoms, within still more complex sugars and nucleotides, within more complex DNA molecules, within complex nuclei, within complex neurons, within the complex human brain, all of which are integrated in a human body. Such “complexification” would be impossible in both a totally chaotic, unstable universe and an utterly simple, homogeneous universe of, say, hydrogen atoms or quarks.
Described by man, Prescribed by God. There is no scientific reason why there should be any laws at all. It would be perfectly logical for there to be chaos instead of order. Therefore the FACT of order itself suggests that somewhere at the bottom of all this there is a Mind at work. This Mind, which is uncaused, can be called 'God.' If someone asked me what's your definition of 'God', I would say 'That which is Uncaused and the source of all that is Caused.'
https://3lib.net/book/5903498/82353b
Stanley Edgar Rickard Evidence of Design in Natural Law 2021
One remarkable feature of the natural world is that all of its phenomena obey relatively simple laws. The scientific enterprise exists because man has discovered that wherever he probes nature, he finds laws shaping its operation.
If all natural events have always been lawful, we must presume that the laws came first. How could it be otherwise? How could the whole world of nature have ever precisely obeyed laws that did not yet exist? But where did they exist? A law is simply an idea, and an idea exists only in someone's mind. Since there is no mind in nature, nature itself has no intelligence of the laws which govern it. Modern science takes it for granted that the universe has always danced to rhythms it cannot hear, but still assigns power of motion to the dancers themselves. How is that possible? The power to make things happen in obedience to universal laws cannot reside in anything ignorant of these laws. Would it be more reasonable to suppose that this power resides in the laws themselves? Of course not. Ideas have no intrinsic power. They affect events only as they direct the will of a thinking person. Only a thinking person has the power to make things happen. Since natural events were lawful before man ever conceived of natural laws, the thinking person responsible for the orderly operation of the universe must be a higher Being, a Being we know as God. Our very ability to establish the laws of nature depends on their stability.(In fact, the idea of a law of nature implies stability.) Likewise, the laws of nature must remain constant long enough to provide the kind of stability life requires through the building of nested layers of complexity. The properties of the most fundamental units of complexity we know of, quarks, must remain constant in order for them to form larger units, protons and neutrons, which then go into building even larger units, atoms, and so on, all the way to stars, planets, and in some sense, people. The lower levels of complexity provide the structure and carry the information of life. There is still a great deal of mystery about how the various levels relate, but clearly, at each level, structures must remain stable over vast stretches of space and time. And our universe does not merely contain complex structures; it also contains elaborately nested layers of higher and higher complexity. Consider complex carbon atoms, within still more complex sugars and nucleotides, within more complex DNA molecules, within complex nuclei, within complex neurons, within the complex human brain, all of which are integrated in a human body. Such “complexification” would be impossible in both a totally chaotic, unstable universe and an utterly simple, homogeneous universe of, say, hydrogen atoms or quarks. Of course, although nature’s laws are generally stable, simple, and linear—while allowing the complexity necessary for life—they do take more complicated forms. But they usually do so only in those regions of the universe far removed from our everyday experiences: general relativistic effects in high-gravity environments, the strong nuclear force inside the atomic nucleus, quantum mechanical interactions among electrons in atoms. And even in these far-flung regions, nature still guides us toward discovery. Even within the more complicated realm of quantum mechanics, for instance, we can describe many interactions with the relatively simple Schrödinger Equation. Eugene Wigner famously spoke of the “unreasonable effectiveness of mathematics in natural science”—unreasonable only if one assumes, we might add, that the universe is not underwritten by reason. Wigner was impressed by the simplicity of the mathematics that describes the workings of the universe and our relative ease in discovering them. Philosopher Mark Steiner, in The Applicability of Mathematics as a Philosophical Problem, has updated Wigner’s musings with detailed examples of the deep connections and uncanny predictive power of pure mathematics as applied to the laws of nature
http://www.themoorings.org/apologetics/theisticarg/teleoarg/teleo2.html
Described by man, Prescribed by God. There is no scientific reason why there should be any laws at all. It would be perfectly logical for there to be chaos instead of order. Therefore the FACT of order itself suggests that somewhere at the bottom of all this there is a Mind at work. This Mind, which is uncaused, can be called 'God.' If someone asked me what's your definition of 'God', I would say 'That which is Uncaused and the source of all that is Caused.' 3
John Marsh Did Einstein Believe in God? 2011
The following quotations from Einstein are all in Jammer’s book:
“Every scientist becomes convinced that the laws of nature manifest the existence of a spirit vastly superior to that of men.”
“Everyone who is seriously involved in the pursuit of science becomes convinced that a spirit is manifest in the laws of the universe – a spirit vastly superior to that of man.”
“The divine reveals itself in the physical world.”
“My God created laws… His universe is not ruled by wishful thinking but by immutable laws.”
“I want to know how God created this world. I want to know his thoughts.”
“What I am really interested in knowing is whether God could have created the world in a different way.”
“This firm belief in a superior mind that reveals itself in the world of experience, represents my conception of God.”
“My religiosity consists of a humble admiration of the infinitely superior spirit, …That superior reasoning power forms my idea of God.”
https://www.bethinking.org/god/did-einstein-believe-in-god
Where do the laws of physics come from?
(Guth) pauses: "We are a long way from being able to answer that one." Yes, that would be a very big gap in scientific knowledge!
Newton’s Three Laws of Motion.
Law of Gravity.
Conservation of Mass-Energy.
Conservation of Momentum.
Laws of Thermodynamics.
Electrostatic Laws.
Invariance of the Speed of Light.
Modern Physics & Physical Laws.
http://yecheadquarters.org/?p=1172
Don Patton: Origin and Evolution of the Universe Chapter 1 THE ORIGIN OF MATTER Part 1
Applying the scientific method:
When all conclusions fit and point into one direction only, what is science supposed to do? According to the scientific method you are supposed to follow the evidence regardless of where it leads, not ignore it because it leads to where you don;t want to go. But science refusal to follow the conclusions of the only things that make sense here is proof that science is not really about finding truth where ever it may lead, but making everything that exists or is discovered conform to what they have already accepted as truth.
Proof? Evolutionists have already exalted their idea of their theory as being a true proven facts with mountains of empirical evidence. They even went as far as to exalt this theory of theirs to being a Scientific theory. The problem here is that there is really no criteria that the theory had to meet to graduate to this level. Nothing. They cannot give us a 1 ,2 ,3 criteria on what the theory had to do to reach this status or the supposed evidence that took it over the top, and how it would maintain this status. How does one know that evolution still meets the criteria of being a scientific theory when evidence for and against are found all the time? And evidence gets proven wrong or found to be fraud but some how the theory of evolution holds to a criteria that is not even clear or written?
Is evolution the hero of the atheist movement?
This is what happens when a person becomes a hero unto the people. They exalt him to a status that he may not be worthy of, and make positive claims about him that are not even true just so they can look up to him as their hero. And they will protect their hero and anyone whom disagrees becomes their enemy. This is what has happened to the theory of evolution. It has become the atheist hero in the plot to justify their disbelief in God. And because the idea is their hero it will be treated as such and becomes something the atheist can look up to whether it meets the criteria or not. And it is protected against all whom would dare to disagree, and those whom disagree become the enemy for that very reason. Why do you think atheists who believe in evolution hate all creationists when they have never met them? The hero complex of evolution requires them to do just that.
http://evolutionfacts.com/Ev-V1/1evlch01a.htm
WALTER BRADLEY Is There Scientific Evidence for the Existence of God? JULY 9, 1995
For life to exist, we need an orderly (and by implication, intelligible) universe. Order at many different levels is required. For instance, to have planets that circle their stars, we need Newtonian mechanics operating in a three-dimensional universe. For there to be multiple stable elements of the periodic table to provide a sufficient variety of atomic "building blocks" for life, we need atomic structure to be constrained by the laws of quantum mechanics. We further need the orderliness in chemical reactions that is the consequence of Boltzmann's equation for the second law of thermodynamics. And for an energy source like the sun to transfer its life-giving energy to a habitat like Earth, we require the laws of electromagnetic radiation that Maxwell described.
Our universe is indeed orderly, and in precisely the way necessary for it to serve as a suitable habitat for life. The wonderful internal ordering of the cosmos is matched only by its extraordinary economy. Each one of the fundamental laws of nature is essential to life itself. A universe lacking any of the laws would almost certainly be a universe without life.
Yet even the splendid orderliness of the cosmos, expressible in the mathematical forms, is only a small first step in creating a universe with a suitable place for habitation by complex, conscious life.
Johannes Kepler, Defundamentis Astrologiae Certioribus, Thesis XX (1601)
"The chief aim of all investigations of the external world should be to discover the rational order and harmony which has been imposed on it by God and which He revealed to us in the language of mathematics."
The particulars of the mathematical forms themselves are also critical. Consider the problem of stability at the atomic and cosmic levels. Both Hamilton's equations for non-relativistic, Newtonian mechanics and Einstein's theory of general relativity are unstable for a sun with planets unless the gravitational potential energy is correctly proportional to, a requirement that is only met for a universe with three spatial dimensions. For Schrödinger's equations for quantum mechanics to give stable, bound energy levels for atomic hydrogen (and by implication, for all atoms), the universe must have no more than three spatial dimensions. Maxwell's equations for electromagnetic energy transmission also require that the universe be no more than three-dimensional. Richard Courant illustrates this felicitous meeting of natural laws with the example of sound and light: "[O]ur actual physical world, in which acoustic or electromagnetic signals are the basis of communication, seems to be singled out among the mathematically conceivable models by intrinsic simplicity and harmony. To summarize, for life to exist, we need an orderly (and by implication, intelligible) universe. Order at many different levels is required. For instance, to have planets that circle their stars, we need Newtonian mechanics operating in a three-dimensional universe. For there to be multiple stable elements of the periodic table to provide a sufficient variety of atomic "building blocks" for life, we need atomic structure to be constrained by the laws of quantum mechanics. We further need the orderliness in chemical reactions that is the consequence of Boltzmann's equation for the second law of thermodynamics. And for an energy source like the sun to transfer its life-giving energy to a habitat like Earth, we require the laws of electromagnetic radiation that Maxwell described.
Our universe is indeed orderly, and in precisely the way necessary for it to serve as a suitable habitat for life. The wonderful internal ordering of the cosmos is matched only by its extraordinary economy. Each one of the fundamental laws of nature is essential to life itself. A universe lacking any of the laws would almost certainly be a universe without life. Many modern scientists, like the mathematicians centuries before them, have been awestruck by the evidence for intelligent design implicit in nature's mathematical harmony and the internal consistency of the laws of nature.
Nobel laureates Eugene Wigner and Albert Einstein have respectfully evoked "mystery" or "eternal mystery" in their meditations upon the brilliant mathematical encoding of nature's deep structures. But as Kepler, Newton, Galileo, Copernicus, Davies, and Hoyle and many others have noted, the mysterious coherency of the mathematical forms underlying the cosmos is solved if we recognize these forms to be the creative intentionality of an intelligent creator who has purposefully designed our cosmos as an ideal habitat for us.
Question: What is their origin? Can laws come about naturally? How did they come about fully balanced to create order instead of chaos?
Answer: The laws themselves defy a natural existence and science itself has not even one clue on how to explain them coming into being naturally.So when you use deductive reasoning, cancelling out all that does not fit or will not work, there is only one conclusion left that fits the bill of why the laws exist, and why they work together to make order instead of chaos.
Deny it as naturalist may, their way if thinking cannot explain away a Creator creating the laws that exist and the fact that they create order instead of chaos. That they are put together and tweaked to be in balance like a formula making everything work together to create all that we see. Always ignoring that even one notch off in how one law works with another that total and complete chaos would be the result. And that they cannot even contemplate the first step in an explanation that would fit their world views.
Laws of Physics, where did they come from?
https://www.youtube.com/watch?v=T8VYZwzLbk8&t=256s
Paul Davies - What is the Origin of the Laws of Nature?
https://www.youtube.com/watch?v=HOLjx57_7_c
Martin Rees - Where Do the Laws of Nature Come From?
https://www.youtube.com/watch?v=vmvt6nn_Kb0
Jerry Bowyer, “God In Mathematics” at Forbes
https://uncommondescent.com/intelligent-design/an-interview-on-god-and-mathematics/?fbclid=IwAR0Z5yG7IXJS786QzW57iLRzpaqhk11J9HAQRWbSpzn6uBHw_khCqGVk1xs

Roger Penrose The Second Law of thermodynamics is one of the most fundamental principles of physics
https://accelconf.web.cern.ch/e06/papers/thespa01.pdf

https://www.quora.com/What-are-the-laws-of-physics
https://quod.lib.umich.edu/e/ergo/12405314.0006.042/--reasonable-little-question-a-formulation-of-the-fine-tuning?rgn=main;view=fulltext
Jacob Silverman 10 Scientific Laws and Theories You Really Should Know May 4, 2021
Big Bang Theory
Hubble's Law of Cosmic Expansion
Kepler's Laws of Planetary Motion
Universal Law of Gravitation
Newton's Laws of Motion
Laws of Thermodynamics
Archimedes' Buoyancy Principle
Evolution and Natural Selection
[url=https://science.howst
Last edited by Otangelo on Fri Mar 11, 2022 4:02 am; edited 96 times in total