Stephen Meyer's new cosmological argument
https://reasonandscience.catsboard.com/t2874-stephen-meyer-s-new-cosmological-argument
Stephen Meyer on Good Questions and a God Hypothesis
https://www.discovery.org/multimedia/audio/2019/08/stephen-meyer-on-good-questions-and-a-god-hypothesis/
Stephen Meyer's new argument is based on astronomical observations. Fine-tuning and cosmological arguments rely on invoking an external cause of the universe. Stephen began, building on the lectures given previously by Richards and Gonzalez on the expansion of the universe and the necessity of a beginning.
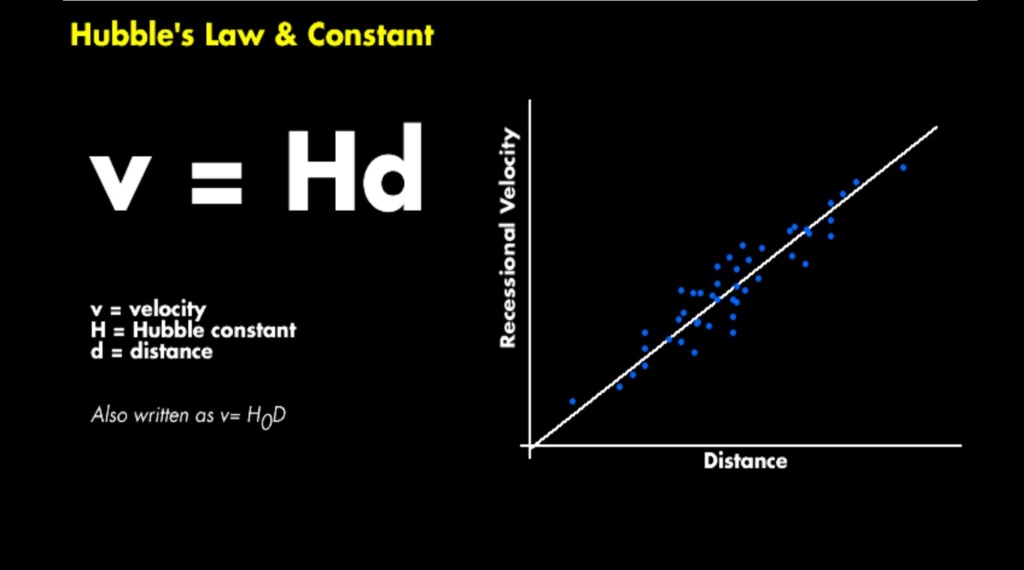
An interesting convergence came in the 1920s after Hubble came up with the Hubble constant, the relationship of the expansion rate, and the distance to distant galaxies.

But who gets less attention is the Belgian priest, Father Lemaitre, in 1927, about what was already known about the redshift, the theoretical physics coming from general relativity, where Einstein the first time introduced the cosmological constant,

but then, later, physicists, Friedman, and Lemaitre himself said: Wait a minute, the value, assigned to the cosmological constant, to get the outward force of expansion, and the contracting force of gravity, is balanced just right, is extremely contrived, and is, therefore, unrealistically fine-tuned,

and the vast range of possible solutions, of possible values for that cosmological constant, that gives a dynamic universe, and since the redshift evidence was already available, LeMaitre said, and he introduced this evidence to Einstein in a Taxicab ride (that's how science was done back then ), and he said:
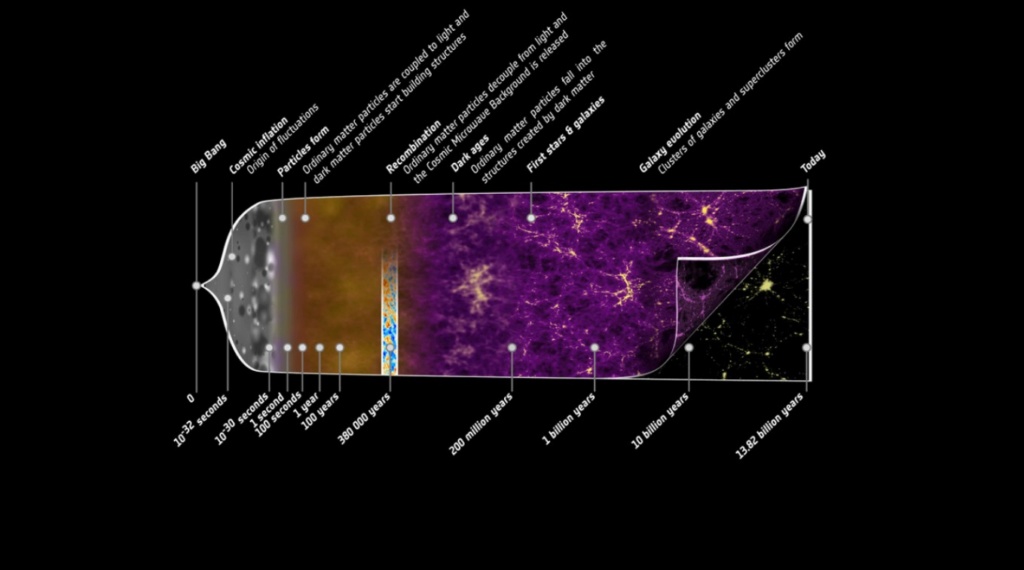
the better solution is a conjoined solution in astronomy and that gives you an expanding universe from some kind of beginning of the expansion. And that's the birth of the Big Bang. That's 1927.

In the sixties, Hawking began to think about Black hole physics. A black hole is a place where the gravitational forces are so intense, they bend space so tightly, that not even light can get out.
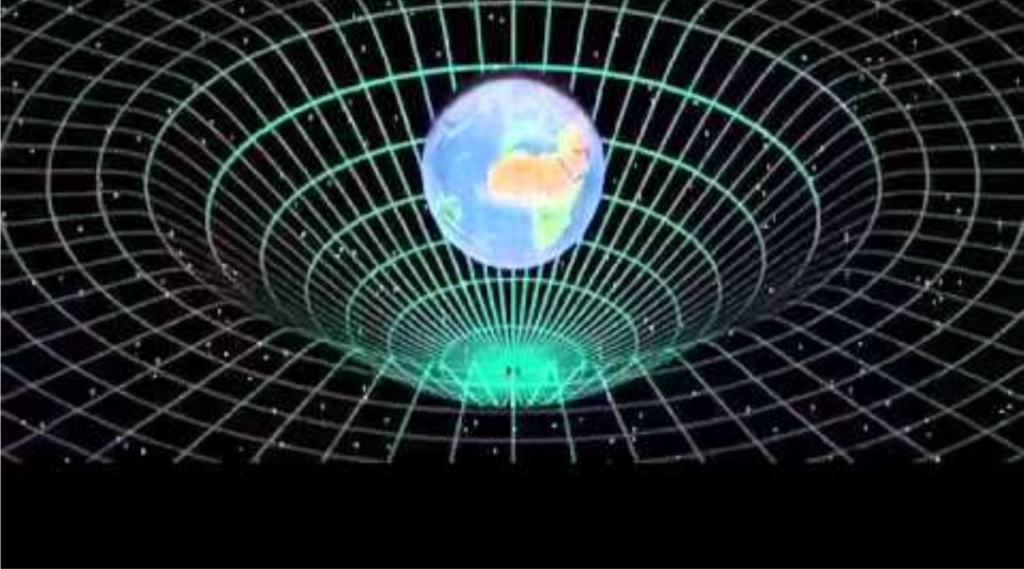
The core concept of general relativity is that matter is actually bending space, is curving space, creates lines of trajectories, even light, as light passes through a massive object, and in fact the way of thinking of general relativity from the field of equations is to think that matter tells space how to curve, and space tells matter, how to move, so this is a reciprocal relationship.

So Hawking is thinking about all this in relation to black holes because a black hole is a place of matter so densely compacted and space is so densely curved that no light can get out, so Hawking has an insight, and says, why do we not apply what we know about black holes and general relativity, to the question of cosmology. To the origin of the universe itself.

If we realize that the universe is expanding outwards, if we extrapolate back, that means that the matter in the universe is getting more and more densely compacted. So more or the same amount of matter, and a smaller and smaller and smaller volume, so space will get tightly curved until eventually, you arrive at some kind of a limit.

So Hawking presented this idea in his PhD. thesis and Penrose said: Congratulations, Dr Hawking, now go out working out the maths. So in 1968 and following, Hawking worked with Penrose and Ellis to prove the singularity theorem, which basically shows that as you go back in time you go to a point where the universe is past geodesically incomplete,
which means there is a beginning in time, and its not perfectly homogeneous, and the universe begins from zero spacial volume, and, basically, everything begins from there.
In order for the conditions of the theorem to be met, the universe cannot be completely homogeneous, which the universe meets. Another matter is which energy conditions neet to apply, and there is an agreement that the energy condition is positive during all the time of this expansion.
But now there is this weird quantum dimension. So when the universe is very very small, it would be indeterministic, and so it is when crossing the point of singularity, some physicists say, well wait, we could have points of fluctuations, that would cause the universe to violate the energy conditions, where you have temporarily a negative energy condition.
And one model adopted the eternal chaotic inflation idea, where the universe expanded very very rapidly, called inflation. But, an extension of that idea was that chaotic inflation had gone infinitely in the past, and was continuing infinitely in the future. And while the inflation goes on, the field, called infinite time field, would occasionally, shut off, just the right measure, and cause all the universe.

That also came associated with the multiverse. So since that inflation was going back infinitely, there was no beginning. Two physicists began to explore that inflation cosmology, Borden and Vilenkin. And they had an initial proof in 1994, that showed that even a chaotic inflation model would have a beginning as well.

Then, in 2003, they developed a model, that was not subject to any energy condition at all, which was called the Borden-Guth-Vilenkin theorem. It is based on special relativity, and what they showed was that

even if the universe is expanding infinitely into the future, it must have had a temporal beginning, it must be geodesically past, incomplete. It traded on quantum indeterminacy, in the very tiny time when the universe was small enough to be described by quantum mechanics. Quantum mechanics is the physicism of the very small, and the very weird.
So, Einsteins ideas give us a very straightforward, a theoretical physics confirmation and an indication of a very beginning, which confirms the testimony of observations astronomy.
Inside that tiny window of Planck time, we have quantum mechanics, so we may not extrapolate back all the way to the beginning, using straightforward mathematical considerations from Einstein's theory of general relativity. We now think about what gravity would be like in the so-called quantum domain, where it's really really small.
And so, theories, that became known as quantum gravity, or quantum cosmology, became a way of go-to when thinking about the origin of the universe, in a post - Einsteinian way, in a domain, where Einstein's physics may not apply. So quantum cosmology is describing the early stages using the maths of quantum mechanics.
So the discussion of the origin of the universe started in the eighties and shifted away from Einstein's general relativity, to better considerations with quantum mechanics.

So the first to work on this was Stephen Hawking. He wrote a book in 1988, called, a brief history of time. So quantum cosmology in addition to the new way of thinking about the origin of the universe has been posed, and it has been posed by Hawking himself as essentially an argument against the Kalaam cosmological argument of Gods existence.

Hawking took that argument and famously said: What need is there for a creator ?! That followed after the presentation of the Hawking Hartle model quantum cosmology.

What they basically claimed was that the laws of the universe came from nothing and that nothing was unstable, this is Lawrence Krauss formulation of it.

Hawking in his last book before he died wrote because there is such a law as gravity, he is speaking about quantum gravitational laws, the universe can and does create itself from nothing. Spontaneous creation is the reason why there is something rather than nothing, why we exist, why the universe exists, is not necessary to invoke God, that set the universe going.
An ordinary person looking at this statement might be tempted to think about something ontological that he is saying here since spontaneous creation means that something happens spontaneously for no apparent reason at all, and then saying, that there is no reason at all, that there is something rather than nothing, and why the universe exists, for no reason at all.
And the problem in Hawking's book is, that you can't really understand, what the argument is.

There is a lot of assertions and analogies, but it's not really going into the physics, at least not in regards to this statement, so let's look a bit more deeply into quantum cosmology.

First, physicists where first uncomfortable why quantum cosmology and the singularity. Hawkins didn't like the implications of the singularity and looking for a way to solve the problem within the confines of physics itself, but secondly, the extrapolation that is involved, in a singularity, is obtained, let's take into account what is called Planck time, the tiny little time, where things are so small, where quantum effects take route,
so, two different versions of quantum cosmology were developed, one is the Hawking- Hartles, where the singularity is eliminated, and the second one is the Borden-Vilenkin, where it proposes to explain the origin of the universe from the singularity, from nothing at all.
In order to understand what these guys are up to, one has to do an excursion back into ordinary quantum mechanics, but nothing is not ordinary at all. Quantum mechanics was describing how waves and particles are essentially two of the same manifestations of fundamental reality.
Fundamental units can act like waves or particles, be it photons or electrons. There was a famous equation, the Schroedinger equation, which was used to calculate the probability that an electron or photon might be at many possible positions, and the electron might be at any point of many possible positions, that consequence is that it might be a wave or particle, so, a couple of these experiments gave us these strange concepts. The first actually in the 19th century.
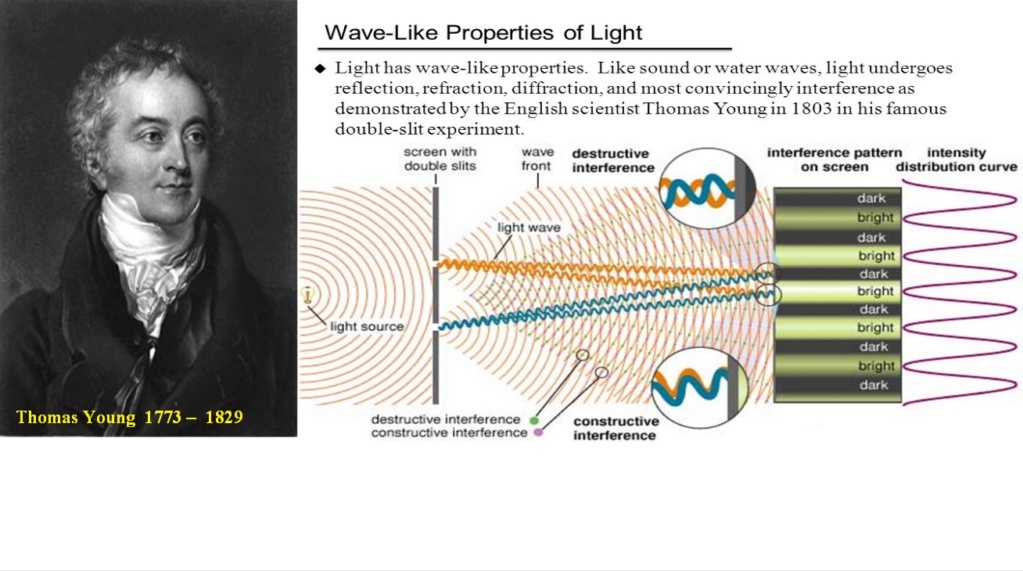
Before 1802, when an experiment was performed by Thomas Young, the famous double-slit experiment, prior it was thought that light is just particles, but light, put through the single and double-slit experiment produced kind of an interference pattern, like concentrating or being less intense, alternately, it was as he dropped something in the water, and it gave waves where they were inforced, where the pit came together or cancelled each other out, where the waves crossed and hit each other.

So that interference pattern characteristic of waves, with light, that suggested that light might be a wave. At the beginning of the 20th century, there was a very interesting experiment made by British physicist Geoffrey Taylor, which made a different version of this double split experiment,
which was able to lower the intensity of light, passing through the double split, where he was able to make that one particle was going through at the time, and what he was able to produce, again, was an interference pattern, that emerged progressively over time, so the light that was manifesting as particles,
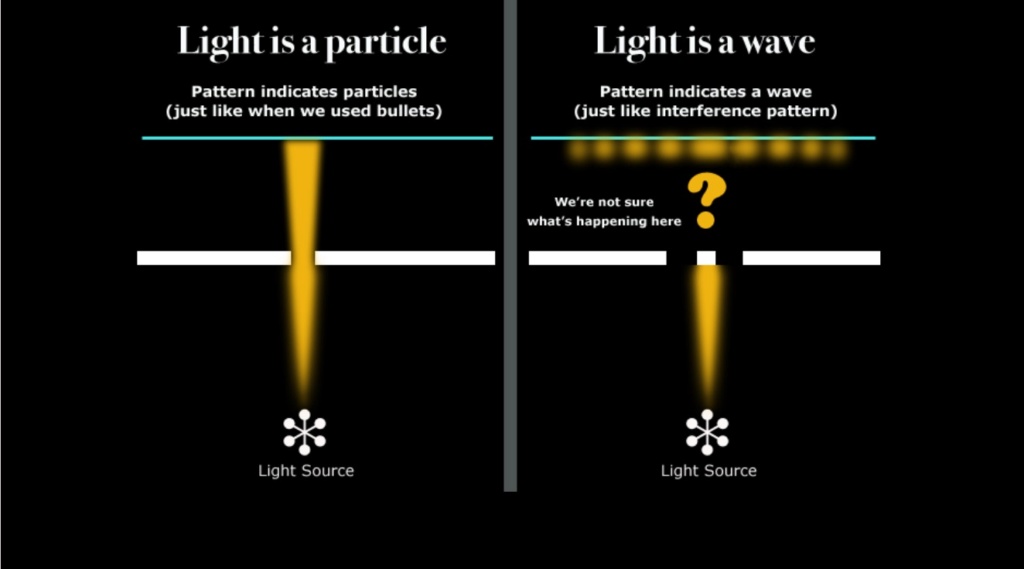
but the longer the particles were collected at the detection plate, the more the interference pattern became evident, suggesting that light even as the individual particles of light that were passing the double slits interfering with themselves, so they were both manifesting wave light and particle light at the same time.
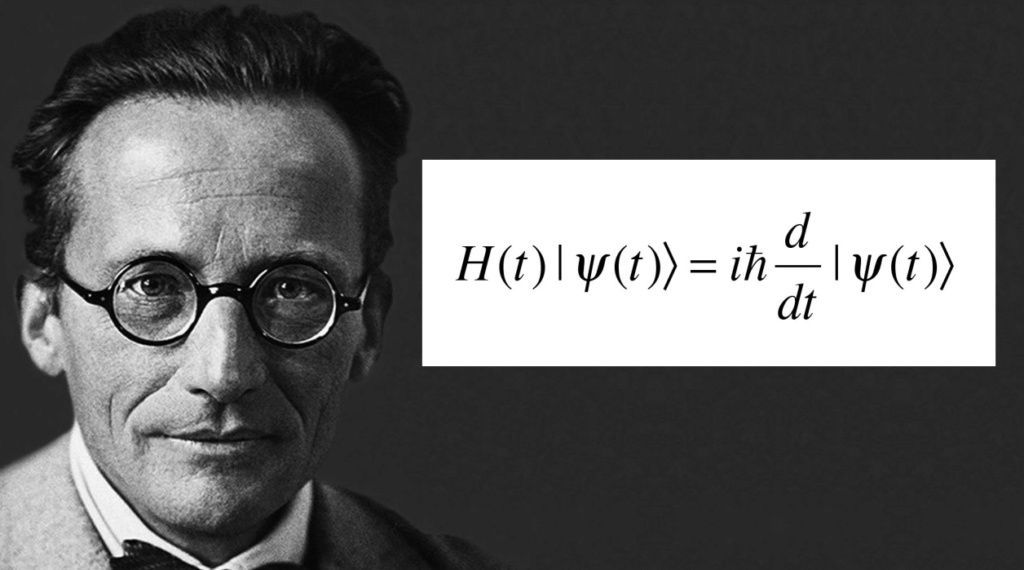
So in order to describe this mathematically, and to get an idea where the particle might show up, manifesting itself at the detection plate, physicists developed the famous mathematics of the Schroedinger equations, which permits us to calculate the probability of the particle manifest itself at a particular point.
The weird thing is that acting itself as a wave until it hits the detection plate it can end up at a whole lot of different places, that is it will not be at any specific place until it is observed, that is the weird thing about quantum mechanics.

Feynman used to say if you think you understand quantum mechanics, well, no, no one really understands quantum mechanics. It's really bizarre. This is the collapse of the wave function. That's ordinary quantum mechanics. All this ordinary quantum mechanics it's even a more exotic situation when it comes to the beginning of the universe.
Quantum mechanics in regular cosmology describes all the possible positions and momenta associated with the waves and particles. In quantum mechanics, the particles can be at one point, even if its smeared out, they can be at lots of different places all at once.
Now, quantum cosmology applies this idea, not to particles and waves of light or electrons, but it defies the idea that different possible geometries and configurations of matter that the universe might have.

We have the shape of our universe, and the configurations of matter are just described by general relativity. General relativity is concerned about the shape of space, and how matter affects them. So there is a matter field, and there is a geometry of space, in general relativity. So we are thinking about the origin of the universe, we are thinking about something intrinsic, about spacial geometry, and the configuration of matter.
Inside Planck Time, we have quantum indeterminacy, so maybe what we are dealing up there, is lots of possible universes, with lots of possible shapes, and geometries, and configurations of matter. And so what happens is, there is a wave theory of equations, the Wheeler-DeWitt equations, which basically synthesizes the Schroeder equation with considerations of Einsteinian gravity, it becomes gravity, plus quantum physics together.
And to describe what the universe might be in that light, in that early dimension of time, it turned to definite characteristics, to a definite expansion.
The philosophical point will be very easy to grasp. There is a kind of conversion, in ordinary quantum mechanics, to describe the equation that describes where the particle can be and allows us to calculate the probabilities associated with whether it is the ones that are observed.
In quantum cosmology, we apply the same kind of math, but you are not looking for particles, you try to calculate the probability at a given type of universe. In particular, ours, because this theory becomes an origins theory, when the equations or the functions, or, this function is the solution to the Wheeler–DeWitt equation.
In ordinary quantum mechanics is a function to describe the probabilities of all the created particles. Lots of different possibilities are described by this function. That function, or the wave function, is a solution in ordinary quantum mechanics for the Schroedinger equation, and in quantum cosmology, its a solution to this Wheeler–DeWitt equation, which is the Schroedinger equation, adapted to try to describe the gravitational fields or possible gravitational fields of the early universe.
So if we can solve these equations, we can get a function that describes all the possible geometries, all the possible shapes that the universe might have, and the different distributions of matter within those shapes. Lots of possible distributions of shapes, lots of possible distributions of matter. So that's the wave function. Quantum cosmologists believe they can explain our universe and in case, that, or if this wave function includes a universe like ours.
Ours is a reasonably probable outcome of this wave function, then we can explain our universe. That's the idea, upon cosmology. So the Wheeler–DeWitt equation is just an analogue to the Schroedinger equation in regular quantum mechanics, describing all the possible, if you solve the equation, you get a side-function to describe all the possible places and the particles could be,
and then if, that's the side function happens to produce or happens to include a universe like ours, explaining the origin of the universe, and without, one place would be without a beginning, as Hawking says, and one would be with a beginning, but coming essentially from nothing. It's just the physics doing the explaining.
We don't need a God hypothesis. We don't need a transcendent cause, the Wheeler–DeWitt equation solves to produce a wave function, ours is included, then we say, the universe emerged out of nothing, out of the physics, the laws of physics now describe, the universe came from, we don't need to invoke God. That's Hawkins argument.

So this is mainly an attempt to address the ultimate cosmological origins questions, without invoking a transcendent cause according to the beginning of the universe. Hawking btw. gets away with a beginning the way he did fix the space-time geometry of the beginning of the universe,
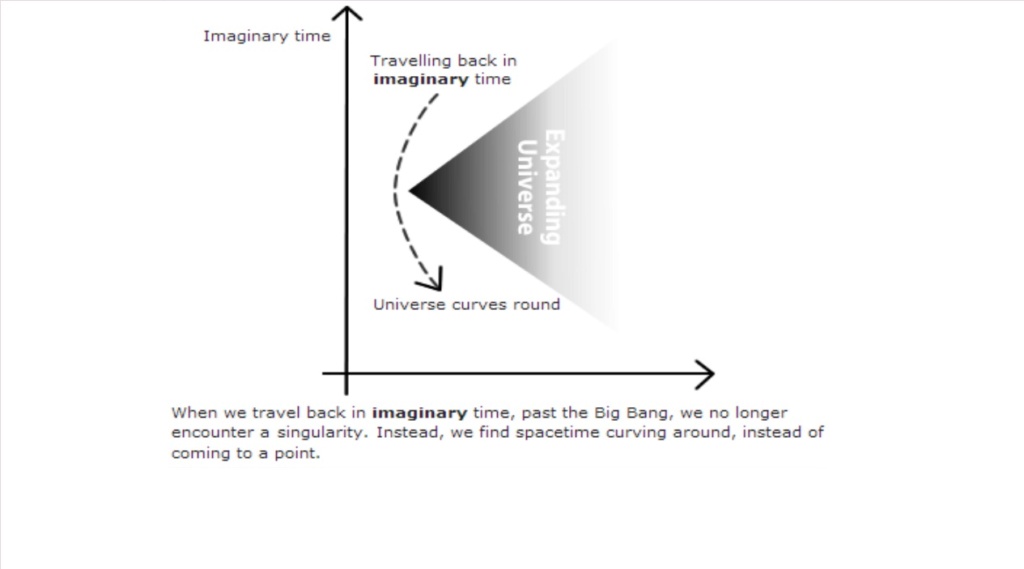
but only by the means of a mathematical trick where he changes the time variable t, and he exchanges it with It, for imaginary time, and so he converts a problem of equation in a real domain into an imaginary domain of complex numbers and solve the problem in complex numbers, and then convert back.
They applied imaginable math and applied it to the real world. And you should not apply real metaphysical implications of what you are doing in an imaginary mathematical domain.

Vilenkins theorem is much more philosophically sensitive, and there is a passage in his book, Many worlds in one, where he is describing the kind of philosophical paradox associated with the whole enterprise of quantum cosmology. He asks this interesting question:

Where does the universe come from? The quantum cosmological answer comes from the side-function. It comes from the universal wave function. Describing all these possible universes, not which actually exist yet, but which are all mathematical possibilities. What does this mean, that the laws are not a mere description of reality, but could have an independent existence of their own, we are talking about the side functions of quantum cosmology.
In the absence of space, time and matter, what tablets could they be written on? The side functions can explain the ways they could exist, it is not a thing yet. The laws are expressed in a form of mathematical equations.

If the means of the equations is the mind, this is mean that mind should create the universe? After he raises this provocative rhetorical question, he completes and doesn't answer us.
Hawking did raise a similar question. Also, in the A brief history of time, he says: what puts fire into the equation that gives a universe to describe? Should mathematical equations have causal power? Are they substantive in the real world? Usually, mathematical equations are what we use to describe the universe.
Wheeler said: One of the equations we construct or dream up, did make things happening in the real world, it is as to say that the latitude and longitude on a real map are responsible for the height of the Himalayan mountains.

The maths in their mind does not cause things to happen in the real world. To say otherwise is a fallacy of ratification. To compute substantial causal powers to concepts. That is as to say that nature has mathematics build into it.

But math is the expression of a powerful mind over nature. But that would be a theistic interpretation.
That is what cosmologists generally won't do. Vilenkin is saying that we need a God. This is sort of the very least point in cosmology, this has an implistic mathematical platonism about. Possible with a theistic twist. We are talking of a mind, pre-existing all of physics, that is pretty close to theism.
There is one more aspect, which is even more profound. We want to explain our universe. That's what the philosophers call the explanandum. The explanandum is a universal wave function that explains our universe as one of the reasonable, probable outcomes. How do we get to that universal wave function? By solving the Wheeler–DeWitt equation.
By solving the Wheeler–DeWitt equation by itself, is a functional differential equation, and that has an infinite number of solutions. How do you solve these equations, by having an infinite number of solutions? You have to restrain the number of solutions. You have to restrain the degree of mathematical freedom, associated with these mathematical equations. And you do that by imposing boundary constraints on the equations.

Let me give an illustration of what that means. There is a law in physics, which is called Poe's law, which describes the harmonic motion of vibrating strings. The law of physics describes the possible harmonic motions, but that does not tell me how hard the string was plucked, that's information extrinsic to the law, that's called an initial condition.
That doesn't tell me how hard a harp player plucked the strings. I have to get that information from observation. From the experiment. Similarly, the string will vibrate differently, depending on how far the bends are. Where they are fixed.
And those are the boundary constraints, particularly in this equation. And that, also, is determined by observation. And you have to know. How the experiment was set up.
So, laws of physics are bound, they get the boundary constraints. You cant get any predictions out of them, you can't get any explanations out of them, you have to know the boundary constraints, and the laws themselves don't give them. That's an additional sort of information.

Think about the fine-tuning. The fine-tuning of those initial conditions. The information has to be provided to the laws in order for them to do any good at all. In any case, in order to solve this big equation, you need to have boundary constraints and the boundary constraints will contain an outcome, that includes our universe is a reasonably probable outcome, which is very precisely chosen.
And Vilenkin does it one way, Hawking and Hartle do it another way. Hawking and Hartle do it with what they call superspace, but the bottom line is, in both cases, both quantum cosmological models, are extremely constrained on degrees of mathematical freedom, are applied to the Wheeler–DeWitt equation, in the wave function, they include a universe like ours, as a reasonably probable argument. How do they choose these boundary rates? It's a bit of a teleological process.

They look forward to the universe they want to, and then they might choose constraints that they get a wave function that includes a universe like that. It's a bit like Dawkins simulation: METHINKS IT IS LIKE A WEASEL He wants to get the Computer program to simulate that directed evolution.
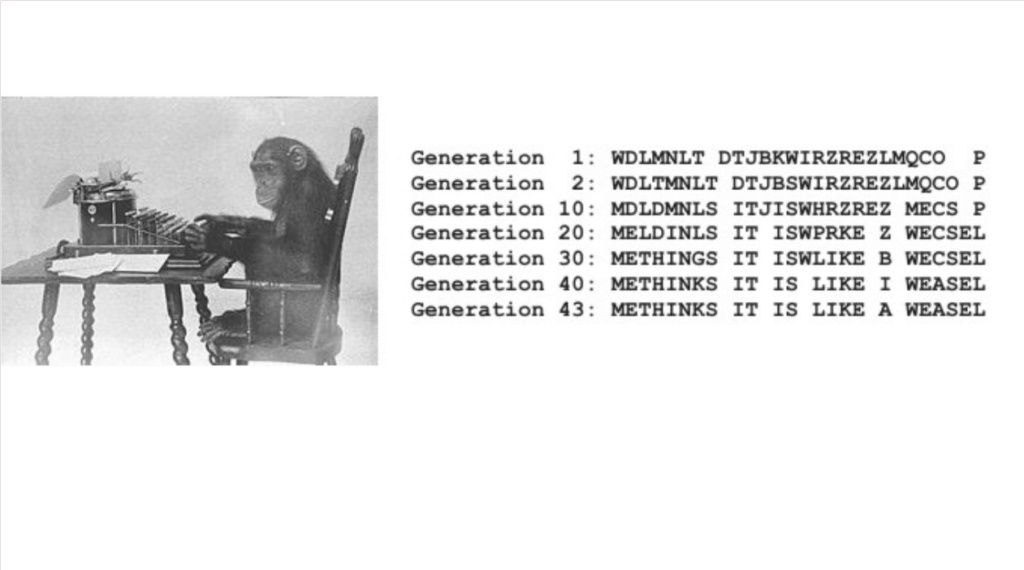
And so he gives it a target sequence, METHINKS IT IS LIKE A WEASEL, and gets the computer program to randomize a string of characters, and he selects those strings that get most similar to those strings he wants, and then he gets eliminating the wrong ones until he gets the outcome he wants. The original sequences have no meaning at all.
So what these guys do, there is some kind of circularity here, where they figure out the universe they want, and then they constrain the solutions to the Wheeler–DeWitt equations and the wave functions, which includes our universe as a possible outcome to get the solution they want.
Obviously, there is circularity in that, there is no problem with modelling ours, but the claim is that this explains the origin of our universe. So, they are doing this modelling. So how does this modelling get off? It gets off by constraining the reason for mathematical freedom. What is that? At the meantime you say: It can be zero or one.
I go and choose one. What if I don't? I constrained it. But I also, in part, I also omit the information. The fundamental definition of a bit of information is chosen between two options, is choosing between.

So what is going on? Theoretical physicists solving the Wheeler–DeWitt equation by infusing information in a form of restricted value constraints, and get an outcome, which is desirable. So what do they actually model? They model for a big amount of information. And in their model, where does information come from?
From the mind of the theoretical physicists themselves.
This reminds me of the origin of life research. Where you have the stimulation experiments. And you know what is a good example? The chemicals are in the bath. Like the byproducts, you get the amino acids, you get a whole lot of other things that you don't want. So what do you do?
Chemically, you remove those other chemicals, so you don't have the interfering cross-reactions, so this is an informed intervention. I want this, not that. All prebiotic simulation experiments are able to move the biochemistry into a life-friendly direction only on the expense of information is being applied by the experimenter. I think that tells us something.

With the expanding universe, that is mathematically analogous. Theoretical physicists providing the information by the boundary constraints, you get the solution that is necessary. This is a fine-tuning problem. The fine-tuning is being manifestly applied or provided by the intelligent physicists. So I think this is actually illustrating the need for mathematical platonism,
I think it actually provides support for intelligent design. So what is being modelled is by intelligence a universe like ours. There are other things that can be said about this, for example, if you take a standard Copenhagen interpretation for example of the collapse of the wave function, what is it that posits the collapse?
It's an observation. What we want to say is, there is a cosmic observer that is responsible for all these possible actualizing universes like ours? Well, no, not for the materialist, so that problem is solved for example by invoking the many-worlds interpretation in quantum mechanics in all possible and impossible worlds but notice, the problem of providing prior information precedes any interpretation of the side function or whatever. So even if you are involved in the mere interpretation of the side function, you still have the problem of getting to the side function, by constraining or increasing the mathematical freedom. There is a big infusion of mathematical information by the theoretical physicists.
If you have a straightforward singularity, you have obviously an infinite of materialistic implications. Borde Guth Vilenkin has pure conditions that have to be met, by establishing a beginning. Hawking - Penrose and Frank Tipler has fewer mathematical conditions that might strengthen the singularity condition, but even if you don't accept the singularity or the past temporal beginning, the reason you would not accept that would be the fact that the universe is behaving like a quantum system in that early time, anyone that is going with a quantum cosmological approach, that has theistic implications, and other reasons. So that is the cosmological trilemma for the naturalists.
https://reasonandscience.catsboard.com/t2874-stephen-meyer-s-new-cosmological-argument
Stephen Meyer on Good Questions and a God Hypothesis
https://www.discovery.org/multimedia/audio/2019/08/stephen-meyer-on-good-questions-and-a-god-hypothesis/
Stephen Meyer's new argument is based on astronomical observations. Fine-tuning and cosmological arguments rely on invoking an external cause of the universe. Stephen began, building on the lectures given previously by Richards and Gonzalez on the expansion of the universe and the necessity of a beginning.

An interesting convergence came in the 1920s after Hubble came up with the Hubble constant, the relationship of the expansion rate, and the distance to distant galaxies.

But who gets less attention is the Belgian priest, Father Lemaitre, in 1927, about what was already known about the redshift, the theoretical physics coming from general relativity, where Einstein the first time introduced the cosmological constant,

but then, later, physicists, Friedman, and Lemaitre himself said: Wait a minute, the value, assigned to the cosmological constant, to get the outward force of expansion, and the contracting force of gravity, is balanced just right, is extremely contrived, and is, therefore, unrealistically fine-tuned,

and the vast range of possible solutions, of possible values for that cosmological constant, that gives a dynamic universe, and since the redshift evidence was already available, LeMaitre said, and he introduced this evidence to Einstein in a Taxicab ride (that's how science was done back then ), and he said:

the better solution is a conjoined solution in astronomy and that gives you an expanding universe from some kind of beginning of the expansion. And that's the birth of the Big Bang. That's 1927.

In the sixties, Hawking began to think about Black hole physics. A black hole is a place where the gravitational forces are so intense, they bend space so tightly, that not even light can get out.

The core concept of general relativity is that matter is actually bending space, is curving space, creates lines of trajectories, even light, as light passes through a massive object, and in fact the way of thinking of general relativity from the field of equations is to think that matter tells space how to curve, and space tells matter, how to move, so this is a reciprocal relationship.

So Hawking is thinking about all this in relation to black holes because a black hole is a place of matter so densely compacted and space is so densely curved that no light can get out, so Hawking has an insight, and says, why do we not apply what we know about black holes and general relativity, to the question of cosmology. To the origin of the universe itself.

If we realize that the universe is expanding outwards, if we extrapolate back, that means that the matter in the universe is getting more and more densely compacted. So more or the same amount of matter, and a smaller and smaller and smaller volume, so space will get tightly curved until eventually, you arrive at some kind of a limit.

So Hawking presented this idea in his PhD. thesis and Penrose said: Congratulations, Dr Hawking, now go out working out the maths. So in 1968 and following, Hawking worked with Penrose and Ellis to prove the singularity theorem, which basically shows that as you go back in time you go to a point where the universe is past geodesically incomplete,
which means there is a beginning in time, and its not perfectly homogeneous, and the universe begins from zero spacial volume, and, basically, everything begins from there.

In order for the conditions of the theorem to be met, the universe cannot be completely homogeneous, which the universe meets. Another matter is which energy conditions neet to apply, and there is an agreement that the energy condition is positive during all the time of this expansion.
But now there is this weird quantum dimension. So when the universe is very very small, it would be indeterministic, and so it is when crossing the point of singularity, some physicists say, well wait, we could have points of fluctuations, that would cause the universe to violate the energy conditions, where you have temporarily a negative energy condition.

And one model adopted the eternal chaotic inflation idea, where the universe expanded very very rapidly, called inflation. But, an extension of that idea was that chaotic inflation had gone infinitely in the past, and was continuing infinitely in the future. And while the inflation goes on, the field, called infinite time field, would occasionally, shut off, just the right measure, and cause all the universe.

That also came associated with the multiverse. So since that inflation was going back infinitely, there was no beginning. Two physicists began to explore that inflation cosmology, Borden and Vilenkin. And they had an initial proof in 1994, that showed that even a chaotic inflation model would have a beginning as well.

Then, in 2003, they developed a model, that was not subject to any energy condition at all, which was called the Borden-Guth-Vilenkin theorem. It is based on special relativity, and what they showed was that

even if the universe is expanding infinitely into the future, it must have had a temporal beginning, it must be geodesically past, incomplete. It traded on quantum indeterminacy, in the very tiny time when the universe was small enough to be described by quantum mechanics. Quantum mechanics is the physicism of the very small, and the very weird.
So, Einsteins ideas give us a very straightforward, a theoretical physics confirmation and an indication of a very beginning, which confirms the testimony of observations astronomy.
Inside that tiny window of Planck time, we have quantum mechanics, so we may not extrapolate back all the way to the beginning, using straightforward mathematical considerations from Einstein's theory of general relativity. We now think about what gravity would be like in the so-called quantum domain, where it's really really small.
And so, theories, that became known as quantum gravity, or quantum cosmology, became a way of go-to when thinking about the origin of the universe, in a post - Einsteinian way, in a domain, where Einstein's physics may not apply. So quantum cosmology is describing the early stages using the maths of quantum mechanics.
So the discussion of the origin of the universe started in the eighties and shifted away from Einstein's general relativity, to better considerations with quantum mechanics.

So the first to work on this was Stephen Hawking. He wrote a book in 1988, called, a brief history of time. So quantum cosmology in addition to the new way of thinking about the origin of the universe has been posed, and it has been posed by Hawking himself as essentially an argument against the Kalaam cosmological argument of Gods existence.

Hawking took that argument and famously said: What need is there for a creator ?! That followed after the presentation of the Hawking Hartle model quantum cosmology.

What they basically claimed was that the laws of the universe came from nothing and that nothing was unstable, this is Lawrence Krauss formulation of it.

Hawking in his last book before he died wrote because there is such a law as gravity, he is speaking about quantum gravitational laws, the universe can and does create itself from nothing. Spontaneous creation is the reason why there is something rather than nothing, why we exist, why the universe exists, is not necessary to invoke God, that set the universe going.
An ordinary person looking at this statement might be tempted to think about something ontological that he is saying here since spontaneous creation means that something happens spontaneously for no apparent reason at all, and then saying, that there is no reason at all, that there is something rather than nothing, and why the universe exists, for no reason at all.
And the problem in Hawking's book is, that you can't really understand, what the argument is.

There is a lot of assertions and analogies, but it's not really going into the physics, at least not in regards to this statement, so let's look a bit more deeply into quantum cosmology.

First, physicists where first uncomfortable why quantum cosmology and the singularity. Hawkins didn't like the implications of the singularity and looking for a way to solve the problem within the confines of physics itself, but secondly, the extrapolation that is involved, in a singularity, is obtained, let's take into account what is called Planck time, the tiny little time, where things are so small, where quantum effects take route,

so, two different versions of quantum cosmology were developed, one is the Hawking- Hartles, where the singularity is eliminated, and the second one is the Borden-Vilenkin, where it proposes to explain the origin of the universe from the singularity, from nothing at all.
In order to understand what these guys are up to, one has to do an excursion back into ordinary quantum mechanics, but nothing is not ordinary at all. Quantum mechanics was describing how waves and particles are essentially two of the same manifestations of fundamental reality.

Fundamental units can act like waves or particles, be it photons or electrons. There was a famous equation, the Schroedinger equation, which was used to calculate the probability that an electron or photon might be at many possible positions, and the electron might be at any point of many possible positions, that consequence is that it might be a wave or particle, so, a couple of these experiments gave us these strange concepts. The first actually in the 19th century.

Before 1802, when an experiment was performed by Thomas Young, the famous double-slit experiment, prior it was thought that light is just particles, but light, put through the single and double-slit experiment produced kind of an interference pattern, like concentrating or being less intense, alternately, it was as he dropped something in the water, and it gave waves where they were inforced, where the pit came together or cancelled each other out, where the waves crossed and hit each other.

So that interference pattern characteristic of waves, with light, that suggested that light might be a wave. At the beginning of the 20th century, there was a very interesting experiment made by British physicist Geoffrey Taylor, which made a different version of this double split experiment,
which was able to lower the intensity of light, passing through the double split, where he was able to make that one particle was going through at the time, and what he was able to produce, again, was an interference pattern, that emerged progressively over time, so the light that was manifesting as particles,

but the longer the particles were collected at the detection plate, the more the interference pattern became evident, suggesting that light even as the individual particles of light that were passing the double slits interfering with themselves, so they were both manifesting wave light and particle light at the same time.
So in order to describe this mathematically, and to get an idea where the particle might show up, manifesting itself at the detection plate, physicists developed the famous mathematics of the Schroedinger equations, which permits us to calculate the probability of the particle manifest itself at a particular point.
The weird thing is that acting itself as a wave until it hits the detection plate it can end up at a whole lot of different places, that is it will not be at any specific place until it is observed, that is the weird thing about quantum mechanics.

Feynman used to say if you think you understand quantum mechanics, well, no, no one really understands quantum mechanics. It's really bizarre. This is the collapse of the wave function. That's ordinary quantum mechanics. All this ordinary quantum mechanics it's even a more exotic situation when it comes to the beginning of the universe.
Quantum mechanics in regular cosmology describes all the possible positions and momenta associated with the waves and particles. In quantum mechanics, the particles can be at one point, even if its smeared out, they can be at lots of different places all at once.
Now, quantum cosmology applies this idea, not to particles and waves of light or electrons, but it defies the idea that different possible geometries and configurations of matter that the universe might have.

We have the shape of our universe, and the configurations of matter are just described by general relativity. General relativity is concerned about the shape of space, and how matter affects them. So there is a matter field, and there is a geometry of space, in general relativity. So we are thinking about the origin of the universe, we are thinking about something intrinsic, about spacial geometry, and the configuration of matter.
Inside Planck Time, we have quantum indeterminacy, so maybe what we are dealing up there, is lots of possible universes, with lots of possible shapes, and geometries, and configurations of matter. And so what happens is, there is a wave theory of equations, the Wheeler-DeWitt equations, which basically synthesizes the Schroeder equation with considerations of Einsteinian gravity, it becomes gravity, plus quantum physics together.
And to describe what the universe might be in that light, in that early dimension of time, it turned to definite characteristics, to a definite expansion.
The philosophical point will be very easy to grasp. There is a kind of conversion, in ordinary quantum mechanics, to describe the equation that describes where the particle can be and allows us to calculate the probabilities associated with whether it is the ones that are observed.
In quantum cosmology, we apply the same kind of math, but you are not looking for particles, you try to calculate the probability at a given type of universe. In particular, ours, because this theory becomes an origins theory, when the equations or the functions, or, this function is the solution to the Wheeler–DeWitt equation.
In ordinary quantum mechanics is a function to describe the probabilities of all the created particles. Lots of different possibilities are described by this function. That function, or the wave function, is a solution in ordinary quantum mechanics for the Schroedinger equation, and in quantum cosmology, its a solution to this Wheeler–DeWitt equation, which is the Schroedinger equation, adapted to try to describe the gravitational fields or possible gravitational fields of the early universe.
So if we can solve these equations, we can get a function that describes all the possible geometries, all the possible shapes that the universe might have, and the different distributions of matter within those shapes. Lots of possible distributions of shapes, lots of possible distributions of matter. So that's the wave function. Quantum cosmologists believe they can explain our universe and in case, that, or if this wave function includes a universe like ours.

Ours is a reasonably probable outcome of this wave function, then we can explain our universe. That's the idea, upon cosmology. So the Wheeler–DeWitt equation is just an analogue to the Schroedinger equation in regular quantum mechanics, describing all the possible, if you solve the equation, you get a side-function to describe all the possible places and the particles could be,
and then if, that's the side function happens to produce or happens to include a universe like ours, explaining the origin of the universe, and without, one place would be without a beginning, as Hawking says, and one would be with a beginning, but coming essentially from nothing. It's just the physics doing the explaining.
We don't need a God hypothesis. We don't need a transcendent cause, the Wheeler–DeWitt equation solves to produce a wave function, ours is included, then we say, the universe emerged out of nothing, out of the physics, the laws of physics now describe, the universe came from, we don't need to invoke God. That's Hawkins argument.

So this is mainly an attempt to address the ultimate cosmological origins questions, without invoking a transcendent cause according to the beginning of the universe. Hawking btw. gets away with a beginning the way he did fix the space-time geometry of the beginning of the universe,

but only by the means of a mathematical trick where he changes the time variable t, and he exchanges it with It, for imaginary time, and so he converts a problem of equation in a real domain into an imaginary domain of complex numbers and solve the problem in complex numbers, and then convert back.
They applied imaginable math and applied it to the real world. And you should not apply real metaphysical implications of what you are doing in an imaginary mathematical domain.

Vilenkins theorem is much more philosophically sensitive, and there is a passage in his book, Many worlds in one, where he is describing the kind of philosophical paradox associated with the whole enterprise of quantum cosmology. He asks this interesting question:

Where does the universe come from? The quantum cosmological answer comes from the side-function. It comes from the universal wave function. Describing all these possible universes, not which actually exist yet, but which are all mathematical possibilities. What does this mean, that the laws are not a mere description of reality, but could have an independent existence of their own, we are talking about the side functions of quantum cosmology.
In the absence of space, time and matter, what tablets could they be written on? The side functions can explain the ways they could exist, it is not a thing yet. The laws are expressed in a form of mathematical equations.

If the means of the equations is the mind, this is mean that mind should create the universe? After he raises this provocative rhetorical question, he completes and doesn't answer us.
Hawking did raise a similar question. Also, in the A brief history of time, he says: what puts fire into the equation that gives a universe to describe? Should mathematical equations have causal power? Are they substantive in the real world? Usually, mathematical equations are what we use to describe the universe.
Wheeler said: One of the equations we construct or dream up, did make things happening in the real world, it is as to say that the latitude and longitude on a real map are responsible for the height of the Himalayan mountains.

The maths in their mind does not cause things to happen in the real world. To say otherwise is a fallacy of ratification. To compute substantial causal powers to concepts. That is as to say that nature has mathematics build into it.

But math is the expression of a powerful mind over nature. But that would be a theistic interpretation.
That is what cosmologists generally won't do. Vilenkin is saying that we need a God. This is sort of the very least point in cosmology, this has an implistic mathematical platonism about. Possible with a theistic twist. We are talking of a mind, pre-existing all of physics, that is pretty close to theism.
There is one more aspect, which is even more profound. We want to explain our universe. That's what the philosophers call the explanandum. The explanandum is a universal wave function that explains our universe as one of the reasonable, probable outcomes. How do we get to that universal wave function? By solving the Wheeler–DeWitt equation.
By solving the Wheeler–DeWitt equation by itself, is a functional differential equation, and that has an infinite number of solutions. How do you solve these equations, by having an infinite number of solutions? You have to restrain the number of solutions. You have to restrain the degree of mathematical freedom, associated with these mathematical equations. And you do that by imposing boundary constraints on the equations.

Let me give an illustration of what that means. There is a law in physics, which is called Poe's law, which describes the harmonic motion of vibrating strings. The law of physics describes the possible harmonic motions, but that does not tell me how hard the string was plucked, that's information extrinsic to the law, that's called an initial condition.
That doesn't tell me how hard a harp player plucked the strings. I have to get that information from observation. From the experiment. Similarly, the string will vibrate differently, depending on how far the bends are. Where they are fixed.
And those are the boundary constraints, particularly in this equation. And that, also, is determined by observation. And you have to know. How the experiment was set up.
So, laws of physics are bound, they get the boundary constraints. You cant get any predictions out of them, you can't get any explanations out of them, you have to know the boundary constraints, and the laws themselves don't give them. That's an additional sort of information.

Think about the fine-tuning. The fine-tuning of those initial conditions. The information has to be provided to the laws in order for them to do any good at all. In any case, in order to solve this big equation, you need to have boundary constraints and the boundary constraints will contain an outcome, that includes our universe is a reasonably probable outcome, which is very precisely chosen.
And Vilenkin does it one way, Hawking and Hartle do it another way. Hawking and Hartle do it with what they call superspace, but the bottom line is, in both cases, both quantum cosmological models, are extremely constrained on degrees of mathematical freedom, are applied to the Wheeler–DeWitt equation, in the wave function, they include a universe like ours, as a reasonably probable argument. How do they choose these boundary rates? It's a bit of a teleological process.

They look forward to the universe they want to, and then they might choose constraints that they get a wave function that includes a universe like that. It's a bit like Dawkins simulation: METHINKS IT IS LIKE A WEASEL He wants to get the Computer program to simulate that directed evolution.

And so he gives it a target sequence, METHINKS IT IS LIKE A WEASEL, and gets the computer program to randomize a string of characters, and he selects those strings that get most similar to those strings he wants, and then he gets eliminating the wrong ones until he gets the outcome he wants. The original sequences have no meaning at all.
So what these guys do, there is some kind of circularity here, where they figure out the universe they want, and then they constrain the solutions to the Wheeler–DeWitt equations and the wave functions, which includes our universe as a possible outcome to get the solution they want.
Obviously, there is circularity in that, there is no problem with modelling ours, but the claim is that this explains the origin of our universe. So, they are doing this modelling. So how does this modelling get off? It gets off by constraining the reason for mathematical freedom. What is that? At the meantime you say: It can be zero or one.
I go and choose one. What if I don't? I constrained it. But I also, in part, I also omit the information. The fundamental definition of a bit of information is chosen between two options, is choosing between.

So what is going on? Theoretical physicists solving the Wheeler–DeWitt equation by infusing information in a form of restricted value constraints, and get an outcome, which is desirable. So what do they actually model? They model for a big amount of information. And in their model, where does information come from?
From the mind of the theoretical physicists themselves.

This reminds me of the origin of life research. Where you have the stimulation experiments. And you know what is a good example? The chemicals are in the bath. Like the byproducts, you get the amino acids, you get a whole lot of other things that you don't want. So what do you do?
Chemically, you remove those other chemicals, so you don't have the interfering cross-reactions, so this is an informed intervention. I want this, not that. All prebiotic simulation experiments are able to move the biochemistry into a life-friendly direction only on the expense of information is being applied by the experimenter. I think that tells us something.

With the expanding universe, that is mathematically analogous. Theoretical physicists providing the information by the boundary constraints, you get the solution that is necessary. This is a fine-tuning problem. The fine-tuning is being manifestly applied or provided by the intelligent physicists. So I think this is actually illustrating the need for mathematical platonism,
I think it actually provides support for intelligent design. So what is being modelled is by intelligence a universe like ours. There are other things that can be said about this, for example, if you take a standard Copenhagen interpretation for example of the collapse of the wave function, what is it that posits the collapse?
It's an observation. What we want to say is, there is a cosmic observer that is responsible for all these possible actualizing universes like ours? Well, no, not for the materialist, so that problem is solved for example by invoking the many-worlds interpretation in quantum mechanics in all possible and impossible worlds but notice, the problem of providing prior information precedes any interpretation of the side function or whatever. So even if you are involved in the mere interpretation of the side function, you still have the problem of getting to the side function, by constraining or increasing the mathematical freedom. There is a big infusion of mathematical information by the theoretical physicists.
If you have a straightforward singularity, you have obviously an infinite of materialistic implications. Borde Guth Vilenkin has pure conditions that have to be met, by establishing a beginning. Hawking - Penrose and Frank Tipler has fewer mathematical conditions that might strengthen the singularity condition, but even if you don't accept the singularity or the past temporal beginning, the reason you would not accept that would be the fact that the universe is behaving like a quantum system in that early time, anyone that is going with a quantum cosmological approach, that has theistic implications, and other reasons. So that is the cosmological trilemma for the naturalists.


